TLSeminar
Project Presentations Schedule
Here is the schedule for the project presentations for Friday, 28 April. Each multi-person team will have up to 20 minutes to present (which should include at least 5 minutes for questions, so plan on a 15-minute or shorter presentation), and each single-person team will have up to 15 minutes to present (which should include at least 3 minutes for questions, so plan on a 12-minute or shorter presentation).
| 9:20-9:30am | Breakfast |
| 9:30-9:50am | Line Of Trust (Anant Kharkar, Sam Havron, Joshua Holtzman, Bethlehem Naylor, Bill Young) |
| 9:50-10:05am | SoK: Software Testing Methods Applied to SSL/TLS: Lessons in Discovering Implementation Bugs (Darion Cassel) |
| 10:05-10:20am | SSLTimer: Testing an SSL Implementation with respect to Timing Attack Vulnerability (Yuchi Tian) |
| 10:20-10:40am | Minimal TLS (Tianyi Jin, Cyrus Malekpour, Bhuvanesh Murali, Daniel Saha) |
| 10:40-10:50am | Break |
| 10:50-11:10am | Quantum Menace (Reid Bixler, Collin Berman) |
| 11:10-11:25am | SSL Skimmer (Adam Imeson) |
| 11:25-11:40am | TIE: TLS Invariants Exploration (Ben Lowman) |
| 11:40am-noon | DecentralizedCA (Bargav Jayaraman, Hannah Li) |
HTTPS Traffic Analysis
Brad Miller, Ling Huang, A. D. Joseph, and J. D. Tygar. I Know Why You Went to the Clinic: Risks and Realization of HTTPS Traffic Analysis, Privacy Enhancing Technologies Symposium, 2014.
Recent research has begun to cast doubt on the confidentiality provided by HTTPS. Researchers from UC Berkeley found that it is possible to determine medical conditions, financial and legal affairs, and sexual orientation of visitors to popular HTTPS-secured websites.
To perform the attack on confidentiality, the researchers employed clustering techniques to reveal traffic patterns and then applied a Gaussian distribution to glean similarities between the targets’ browsing pattern and the researchers’ own traffic patterns. As part of the attack, the researchers needed to visit the same websites as the targets and provide combinations of inputs until their traffic patterns matched those of the targets, within a statistical range of error. They note that ISPs and large government organizations could feasibly gain access to such traffic patterns despite the low probability of another Internet user doing so.
Through detailed traffic analysis, third parties could theoretically fingerprint Internet users and extract valuable personal information from HTTPS-secured communications by exploiting a side channel—in this case, as in many others, timing information.
What’s more, this example is by far the only side-channel leak regarding HTTPS traffic—at least four other prominent works (the latest of which was published just this year!) examine multiple usage scenarios ranging from Netflix viewing history to search queries to Google Map requests:
- Andrew Reed, Michael Kranch. Identifying HTTPS-Protected Netflix Videos in Real-Time. CODASPY 2017.
- Shuo Chen, Rui Wang, XiaoFeng Wang, Kehuan Zhang. Side-Channel Leaks in Web Applications: a Reality Today, a Challenge Tomorrow. 31st IEEE Symposium on Security and Privacy (“Oakland”) 2010.
- IOActive Blog. I can still see your actions on Google Maps over SSL. February 2012.
More Traffic Analysis
TLS traffic analysis can be applied in many scenarios, including:
- Distinguishing between clients on the fly
- Forensics
- Intrusion detection
- Malware detection
- Homogeneous platform verification
- Honeypots
Techniques such as deep packet inspection and TLS flow fingerprinting can be used to distinguish clients, identify whether the encrypted connection is attributed to a Malware or not, and also be used for forensics, intrusion detection and homogeneous platform verification.
TLS fingerprinting
Brotherston, L. (2015). Stealthier attacks and smarter defending with TLS fingerprinting.
During an TLS handshake, most clients initiate a TLS handshake request in a unique way. TLS fingerprinting is usually used to recognize a particular client. In TLS fingerprinting, some elements of the Client Hello Packet are filtered and collected to build a database of signatures. The collected elements are usually the combination of TLS version, record TLS version, ciphersuites, compression options, list of extensions, elliptic curves and signature algorithms. The use of this combined elements is not only reliable in terms of remaining static for any particular client, but offers greater granularity than assessing ciphersuites alone, which has a substantially larger quantity of fingerprint collisions.
IPSec in IPv6: light at the end of the (VPN) tunnel?
IPv6 is the latest version of the Internet Protocol (IP), and the future of the Internet’s identification and location systems; it is slowly overtaking its widely used predecessor, IPv4, and promises to add significant security improvements in the form of the IP Security specification (IPSec). IPSec is a suite which authenticates and encrypts packets of data through a VPN tunnel over a network connection; a version of IPSec has been adapted for IPv4, though the issues we consider concern IPSec’s vulnerabilities in IPv6.
IPSec gateways
A vulnerability in IPSec gateways were recently uncovered as the “Packet Too Big”-“Packet Too Small” ICMP attack in GLOBECOM 2014. As described in the paper, an attacker with eavesdropping and injection access to IPSec encrypted packets can force an IPSec gateway to drop to its minimum possible transmission specification (Path Maximum Transition Unit) and cause major performance penalties and denial of service to the host. The root cause of the attack is in the impossibility of IPSec to distinguish legitimate ICMP packets from illegitimate packets, as well as several contradictions the Path MTU is managed by end hosts when the MTU is below the minimum packet size.
VPN vulnerabilities in IPSec
Vasile C. Perta, Marco V. Barbera, Gareth Tyson, Hamed Haddadi, and Alessandro Mei. A Glance through the VPN Looking Glass: IPv6 Leakage and DNS Hijacking in Commercial VPN clients. Privacy Enhancing Technologies 2015.
A paper in PETS 2015 uncovered several vulnerabilities in IPv6 traffic, including leakage and DNS hijacking. The vulnerability relies on the nature of IPv4/6 dual stack implementations on common operating systems.
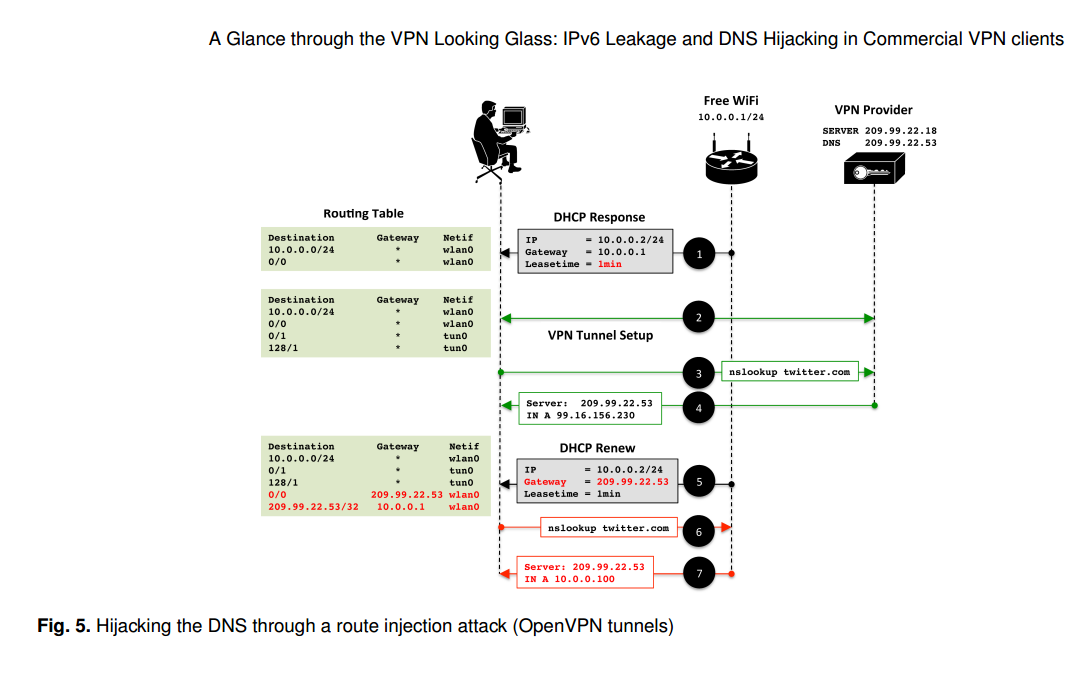
Source: Perta et al., PETS 2015.
All VPN services surveyed rely on the correct configuration of the operating system’s routing table. Worryingly, no attempt is made to secure this operation. The simplest scenario is where the VPN client does not change the victim’s default DNS configuration (e.g., HideMyAss over OpenVPN). In this case, subverting DNS queries is trivial. The access point can simply use DHCP to set the victim’s DNS server to one that it manages itself. The adversary will then receive all DNS queries generated by the host.
The paper notes that “The simplest countermeasure to IPv6 leakage is disabling IPv6 traffic on the host.” Perhaps more sensibly, VPN clients could alter the IPv6 routing table to capture all traffic and prevent leakage from occurring.
QUIC (Quick UDP Internet Connections)
Internet today relies on TCP as a backbone for secure connections over the web. But TCP protocol introduces latency due to synchronization for channel setup, even before TLS handshake. The figure below shows that an average TCP connection takes 56 ms before the TLS handshake begins. This type of latency is not acceptable in mobile devices or in an area with poor internet reception.
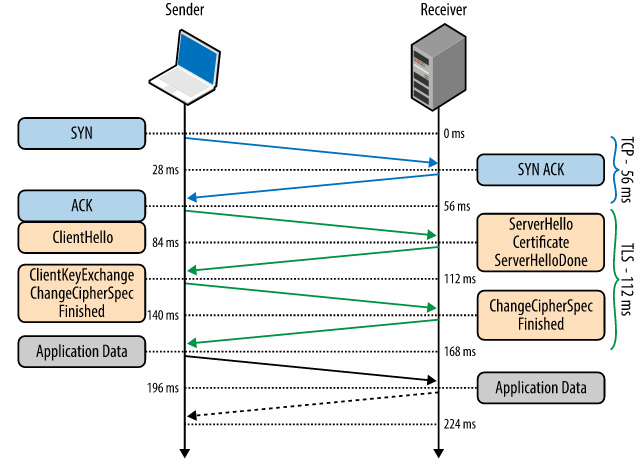
TLS Handshake Time (Source: https://hpbn.co/transport-layer-security-tls/)
This motivates the need for faster secure networking by reducing the number of round trips required to establish secure connection. QUIC aims to achieve this by using UDP as backbone instead of TCP.
Implementing QUIC
QUIC was introduced by Google and it relies on UDP for fast secure connection. UDP provides quick connection and can handle out of sequence packets but requires resending of failed packets to prevent packet loss. It is an excellent alternative for faster secure connection if security is taken care by the application and leaving UDP to take care of the packet transmission and recovery. This requires both server and client side change in application logic to ensure security. Google has already implemented its crypto-layer and provides experimental libraries like libquic and goquic, but currently this can only be tested on Google servers.
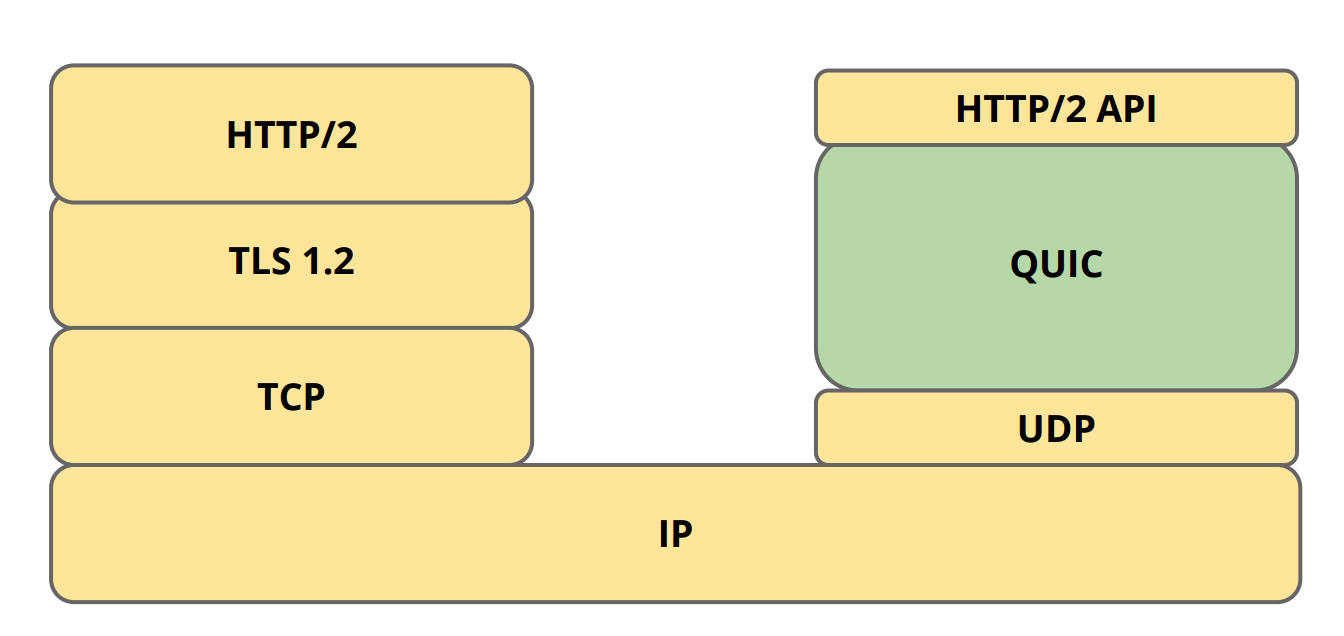
QUIC Protocol Stack (Source: https://ma.ttias.be/googles-quic-protocol-moving-web-tcp-udp/)
InterPlanetary File System (IPFS)
Looking forward to the future of web, it is possible that new models of the Internet will come into play. One such candidate model that is being developed today is the InterPlanetary File System (IPFS). The goal of IPFS replace the Hypertext Transfer Protocol (HTTP) and treat the web as though it is a filesystem and to make the web distributed. Let’s unpack what this means and what IPFS can potentially do for the web.
The Web, Distributed
A key distinction to make between models of the web are the way “nodes,” or computers are linked together. On one end of the spectrum there is the centralized model where a single server contains all the content on the web and every computer must connect to it to retrieve a particular page. If this sounds dystopian and inefficient, it is. This single server would essentially have full say over what content gets to appear on the web and who gets access to it. Thankfully, that is not the model of the web we live under.

On Distributed Communications - Baran
Our web is better described as a decentralized network. There is no central authority in charge of all of the data on the web. Rather, there are millions of servers that host web pages that anyone can access (most of the time). Anyone can create a server and host whatever they want. As the web has evolved however, we see that this model is perhaps not as ideal as we might like; most of the servers that make up the web are controlled by a few server-providers such as Amazon, Google, and Microsoft. The servers of large corporations such as Facebook tend to function as content repositories for billions of people instead of each person controlling his or her identity on the web. As such, the network can be described with a long tail distribution:
Long Tail Distribution
A few servers have the most traffic and the traffic of the remaining servers exponentially decreases and trails off to nil.
What IPFS proposes to do is to create a distributed internet, where the actual distribution of content is done on a peer-to-peer basis. All of the nodes in the network host a nearly-equal amount of content. So why is this good? In both the centralized and decentralized case, a computer must download a file from a single server and deal with that servers busyness. With a distributed network, the computer can instead download content simultaneously from many of its peers. With video delivery for example, the P2P approach could save up to 60% in bandwidth costs.
The Web, Preserved
The second idea that makes IPFS different is that it has historic versioning built in. If you’re familiar with git and the way each file has a history associated with it, then this concept should be right at home for you. If not, then imagine it this way: say you run a blog and one day you decide to add a new post to it. Both the way your blog was without the new post and the way it is now with the new post are saved within the network. So why is this a good thing? Take the case of Yahoo GeoCities. Back in the early 2000s Yahoo provided GeoCities as a place where people could set up small websites and publish content to them. However in 2009 Yahoo decided that GeoCities was no longer a profitable business for it and shut it down. At the time there where about 38 million user-built pages on GeoCities. Any content that was not preserved by the Internet Archive was lost.
How It Works
When someone adds a file to the IPFS network, all of the blocks within the file are hashed. IPFS deduplicates files on entry so if any of the blocks are duplicates of some other block (as shown by comparing the hashes of the blocks), the duplicate block will not be re-added to the network. As mentioned, version history is tracked for every file so the blocks are given a version number (v1 in this example). The file is then distributed across the network to nodes that are “interested in it.” This means that only nodes set to store a particular topic will store the file and its blocks. Indexing information is also stored with each node so that the network as a whole is aware of which node is storing what information. If a lookup is done on the file then the network is queried for nodes storing the content corresponding to the unique hash associated with the file. If you are more interested in how IPFS works, I recommending taking a look at the IPFS whitepaper.
Will it Work?
Technically, yes. The IPFS network is an actual thing that one can join and use now but it remains to be seen whether IPFS can gain widespread adoption. Currently, one of the major problems the network faces is that it is slow both for storing and querying content. This is partially due to the small size of the network, but also because of the overhead that comes from all of the necessary information, like the hashing of the files and their blocks, needed to support the network’s functionality. Perhaps the largest problem is the deep entrenchment of the HTTP protocol. Nearly everything on the web uses HTTP for transporting content, and unless there is a clear and present need for a switch to a different architecture, IPFS may remain wishful thinking for a long while.
Multi-Context TLS
David Naylor, Kyle Schomp, Matteo Varvello, Ilias Leontiadis, Jeremy Blackburn, Diego Lopez, Konstantina Papagiannaki, Pablo Rodriguez Rodriguez, and Peter Steenkiste. Multi-Context TLS (mcTLS): Enabling Secure In-Network Functionality in TLS. SIGCOMM 2015.
Normal TLS facilitates connections between only 2 communicating parties. However, in the wild, most connections pass through various middleboxes along the way that provide additional functionality, such as intrusion detection and parental controls. Current TLS connections with middleboxes require the middlebox to generate fake certificates for the intended site. The network administrator sets up each machine on the network with a custom root CA for the fake cert. The middlebox then connects to the site, meaning that the client doesn’t know what happens in this part of the connection (ex: the middlebox could downgrade the connection).
In order for TLS to support middleboxes, it must incorporate two principles: least privilege and endpoint agreement.
Least Privilege
Multi-Context TLS (mcTLS) implements least privilege by defining 3 types of connection users: readers, writers, and endpoints. In this setup, the endpoints are the client and the target server, while readers and writers are middleboxes. Readers have the least privilege (read-only), writers have additional wite privileges, and endpoints have full access to the network traffic. In mcTLS, readers encrypt the data and generate a MAC for the ciphertext. This MAC verifies that no 3rd-parties modified the data. Writers then create a second MAC for the reader traffic (ciphertext + reader_MAC), which confirms that the readers did not modify the data (since readers do not have write access). Finally, the endpoint also creates a MAC on the entire stream to act as a signal of whether any writers modified the data (although they do have permission). Readers and writers only receive the keys that they need to perform their operations, whereas enpoints receive all keys.
- MAC
- Readers encrypt data, create MAC
- Writers create MAC - verifies no 3rd parties modified data
- Endpoints create MAC - signal of whether writers modified data (they are allowed to)
- Readers, writers only get keys they need - endpoints get all keys
Endpoint Agreement
mcTLS key distribution implements the principle of endpoint agreement. Each middlebox (reader or writer) only receives a subset of the connection keys determined by its functionality. Permissions, which are substantiated through the keys, must be explicitly granted to a middlebox by both the client and server. Each side (client and server) provides each middlebox with half of each key granted by that side’s policy. The middlebox can only use keys (permissions) granted by both the client and server. Thus, the mcTLS Handshake Protocol includes key distribution for the middleboxes in addition to the client and server.
Performance
mcTLS requires most keys to be distributed and therefore involves larger packets in the handshake. This packet size increases with the number of encryption contexts (permissions) and the number of middleboxes. However, the hanshake includes the same number of trips as the standard TLS handshake and therefore requires roughly the same amount of time.
As the web evolves, taking on physical form with embedded devices, or becoming more abstracted with cloud computing, the question of how to secure these new kinds of connections becomes paramount. Can TLS work for non-web scenarios?
Sizzle and DTLS improve TLS performance in an attempt to make the protocol feasible on embedded devices with limited power and bandwidth - but sacrifice some security in the process. Developers of non-browser software like Cloud services, mobile apps, and payment transfer services misunderstand or intentionally disable vital security measures - and SSL APIs fail to communicate how to secure connections and implement authentication. Meanwhile, Amazon Web Services offers a heavily centralized alternative to securing the Cloud and IoT devices - but potentially at a high privacy cost.
Sizzle: TLS For Embedded Devices
Vipul Gupta, Matthew Millard, Stephen Fung, Yu Zhu, Nils Gura, Hans Eberle, Sheueling Chang Shantz. Sizzle: A Standards-based end-to-end Security Architecture for the Embedded Internet. Pervasive and Mobile Computing, 2005.
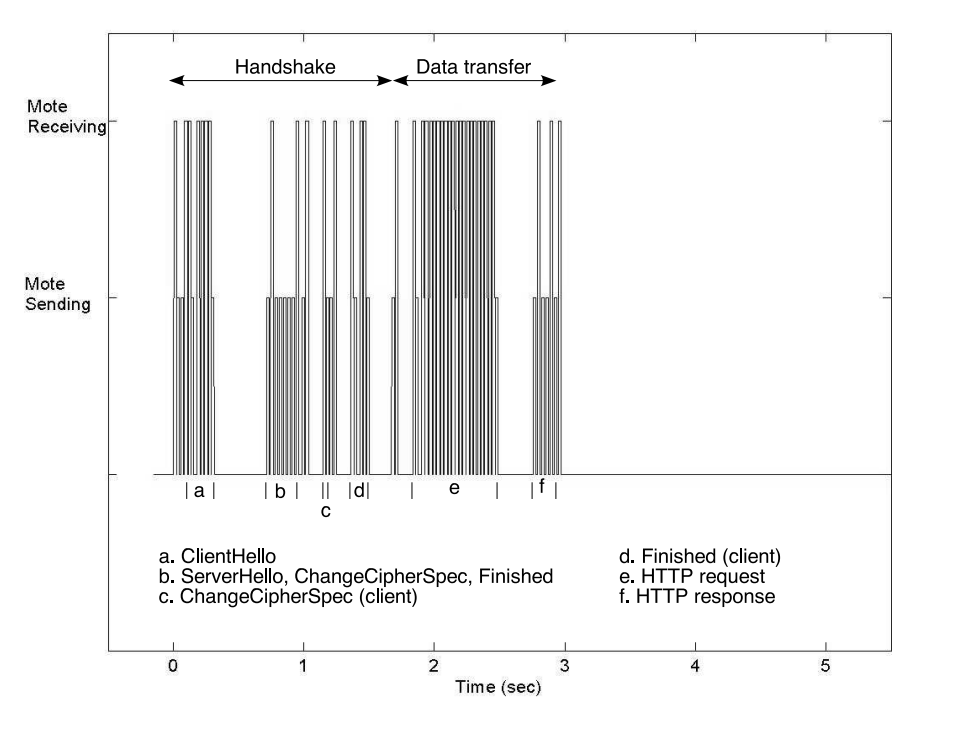
Sizzle is an end-to-end security architecture for embedded devices that is fully implemented on the 8-bit Berkeley/Crossbow Mica2 “mote” platform. Capable of completing an abbreviated SSL (TLS 1.0) handshake in less than 4 seconds, this mote devices were envisioned to function as sensors/actuators connected to the wireless network. When this paper was published (2005), Sizzle on “mote” was the world’s smallest and least resource-intensive secure web server.
With the goal of allowing highly constrained embedded devices to offer secure connections, the authors of this paper uses 160-bit elliptic curve cryptography (ECC) to reduce computation for the system. When using ECC over RSA, there is a 4x speedup (or 5x speed up with session reuse) in computation speed of public/key cryptography. The figures 1 (full handshake) and 2 (abbreviated handshake) below show the comparison of the amount of time it took to transfer 450 bytes of data over HTTPS.
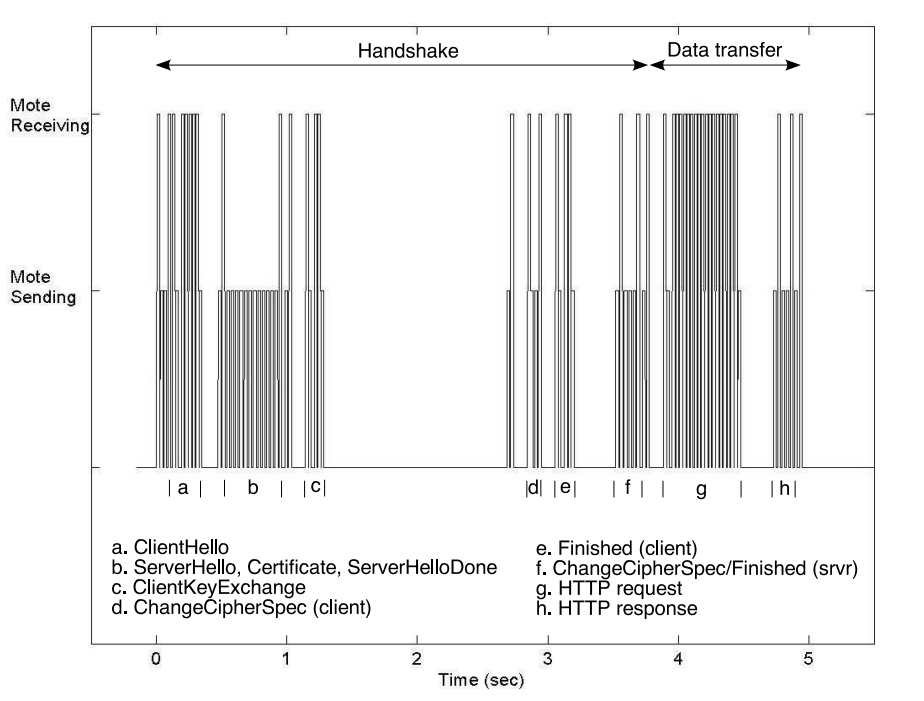
Authentication for the Internet of Things
Thomas Kothmayr, Corinna Schmitt, Wen Hu, Michael Brünig, Georg Carle. DTLS based security and two-way authentication for the Internet of Things. Ad Hoc Networks. May 2013.
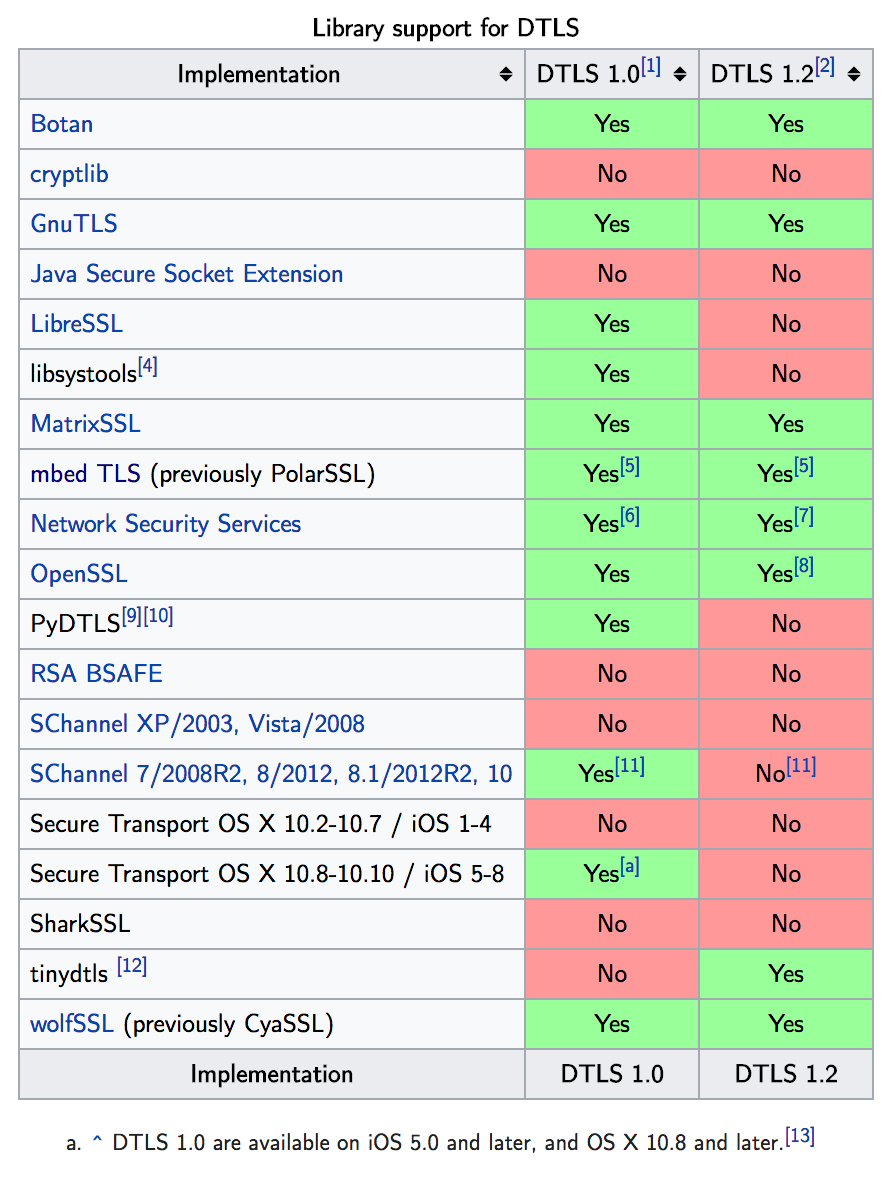
Datagram TLS, also known as DTLS, is for all intents and purposes a “lightweight” version of TLS that can operate on devices that aren’t as powerful as traditional computers. Hence, it was a great addition for the internet of things devices as that revolution took off. According to its specification, it provides the same security guarantees as TLS except it is a stream-oriented service. It, however, does come with a downside. Namely, there is an overhead: tolerance for packet reordering and datagram loss. The former is pretty self explanatory, the latter is essentially stating that if the data is larger than the size of the datagram, it is possible that there be a data loss. Unlike, TLS, there are much fewer libraries that support this protocol, as can be seen in the graphic below:
So, we know of the following encryption techniques. When you have an access point and say a printer, that have a pre-shared key, we use WPA as a communication medium. Similarly, when we need secure connection between a sensor and a security end-point we use VPN, but what about a secure connection using TLS among the internet of things. That is the primary problem that DTLS seeks to solve. Since TCP and TLS incurs an overhead small, battery-starved, low-bandwidth devices, we choose to look at DTLS which uses a less strenuous UDP protocol and a lighter version of TLS, but still maintains the security guarantees.
Earlier, we discussed Sizzle, but it was important to notice that sizzle only provides one-way authentication between the client and the node. That is say you have a thermostat, this would allow someone to change your thermostat, but wouldn’t allow them to read the information. This is not exactly the security that we want.
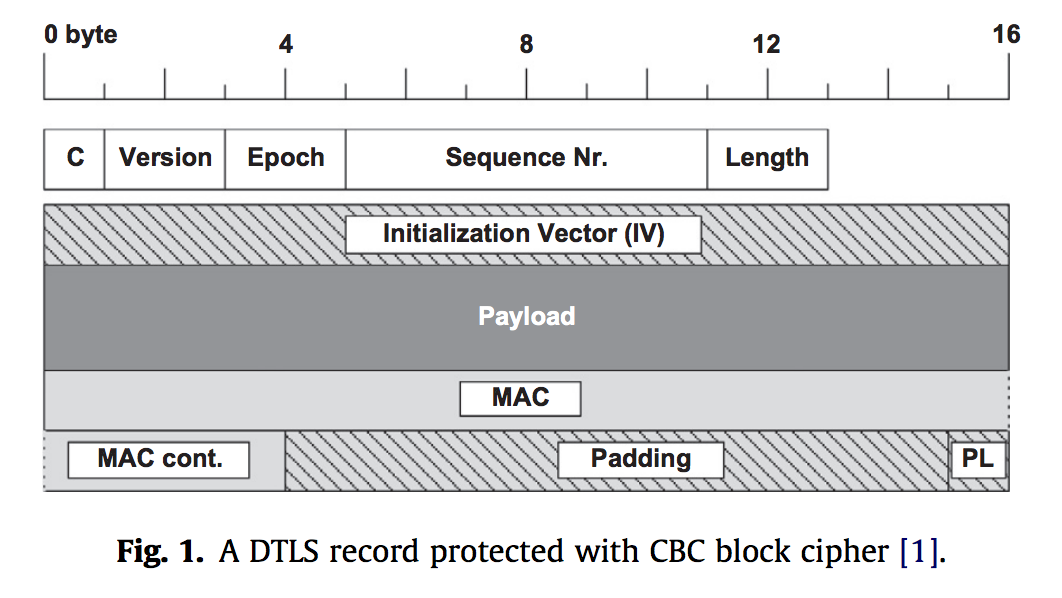
Let’s take a closer look at DTLS. The image below depicts a DTLS record. This looks similar to the record that we have seen with TLS and so there doesn’t seem to be too many causes for concern or intrigue about this structure. To its right, we have the handshake protocol. The main thing to notice here is that we have an extra, optional ClientHello and ClientHelloVerify before the rest of the protocol, which matches with what we’ve seen all semseter with TLS.

This security protocol is an application-layer security protocol. The reasons for using this are that lower-layer security protocols do not provide end-to-end encryption and the secure connections must be established to form a mesh network. This is better than routing algorithms that are agnostic of the payload protection, which means that you may have data sent over a non-secured connection or node.
Finally, we can see how the proposed system actually works. This system uses a system of publishers and subscribers. Each of these can be considered the entities in the secured network. There is an access control server which stores teh access rights for all teh publishers (or motes). To intiialize any connection, the subscriber is verified by access control and is granted a ticket. The subscriber then presents this ticket to the publisher and the publisher verifies its legitimacy setting up the connection. In the larger scheme of things, the connection may look like:
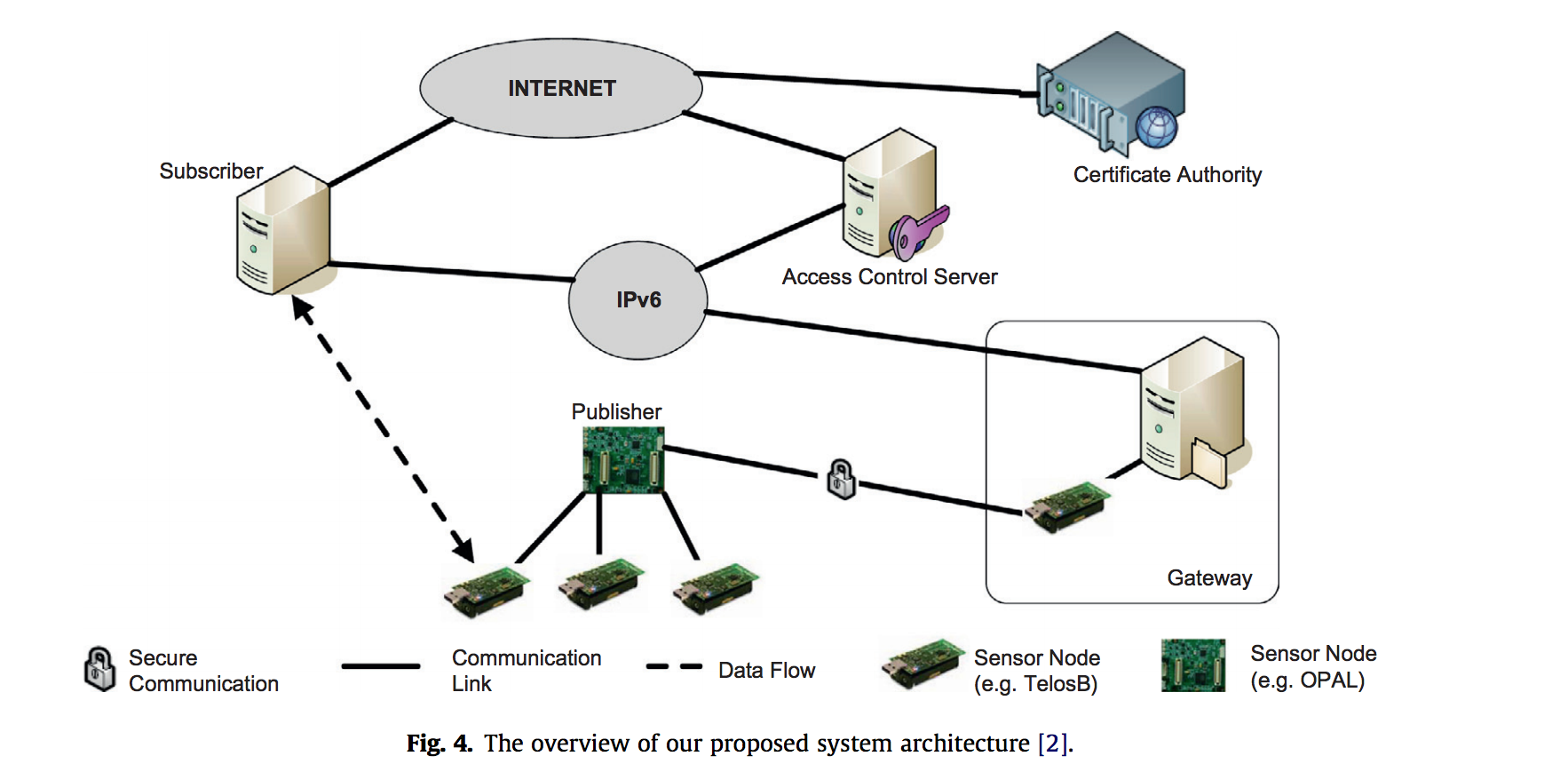
Source: DTLS based security and two-way authentication for the Internet of Things
So overall, when looking at the internet of things, we need to be wary of achieving performance, energy consumption, memory and other limiting factors that the hardware has in order to achieve some level of security. Through DTLS, the researchers presented they were able to create a system that was fairly secure and was able to experience speedups of up to 163 milliseconds based on the protocol and encryption being used. Overall, we are able to see that creating a secure network for the internet of things is slowly manifesting into a reality.
The Most Dangerous Code In The World
Martin Georgiev, Subodh Iyengar, Suman Jana, Rishita Anubhai, Dan Boneh, Vitaly Shmatikov. The Most Dangerous Code in the World: Validating SSL Certificates in Non-Browser Software. ACM CCS 2012.
SSL verification for non-browser applications is nearly always compromised. These applications don’t implement SSL directly, but rather use libraries or wrappers which can have various flaws and vulnerabilities. These added vulnerabilities exist for a variety of reasons, but many of them are introduced because of a lack of security understanding in app developers and poor APIs. Rather than high-level security properties of network tunnels, many APIs divulge low-level details of SSL protocol to app developers. In many cases, options values associated with API functions are misinterpreted by app developers, leading to security risks. In other cases, attempts to fix certificate validation bugs can lead to further insecurity, potentially leading the app developer to accidentally break or disable the certificate validation entirely.
While most apps should do chain-of-trust and hostname verification, few do either. Chain-of-trust is often bypassed altogether, and hostname verification is often done via Common Name instead of SubjectAltName as is recommended by RFC 2818. Many applications also do not have a robust system for checking certificate revocation or allowing the user to do so. OpenSSL provides chain-of-trust verification, but requires that applications do their own hostname verification, while JSSE may or may not do either. This dependency on app developers to understand and implement potentially complex verification is unreasonable and leads to security vulnerabilities.
To avoid shop-for-free attacks, many vendor websites use SSL tunnels to communicate sensitive payment information, and these tunnels are often not set up securely. Attacks were attempted in a controlled environment on these tunnels using self-signed certificates and incorrect Common Name certificates. In Amazon’s flexible payment service, false was sent to cURL in a parameter instead of 2. In a bug fix, this parameter was changed to true, which also bypasses Common Name checks and causes vulnerability to MitM attacks.
One issue for app developers is needing to test their applications before making them live, and for those tests they either need to get valid localHost certificates (which aren’t given out) or they have to disable their certificate validation. Developers often do not enable the validation afterward and “disabling proper certificate validation appears to be the developers’ preferred solution to any problem with SSL libraries.”
App developers should attempt testing using abnormal and invalid certificates. They should also protect themselves by not relying on libraries and not disabling certificate validation during testing. SSL library developers should also attempt to be more explicit about their functionality and should avoid giving responsibility for validation to app developers.
AWS IoT Security Overview
Amazon Web Services (AWS) is the largest cloud service provider in the world, offering a wide range of products from computing and network resources to game development services. One of their newer offerings, AWS IoT, enables developers to link internet-connected devices to the cloud.
The use case for this service is the Internet of Things. Physical sensors in our homes, offices, and cities collect data from their surroundings. Software can then analyze this data and leverage actuators to effect changes in the environment. For example, smart thermostats use temperature sensors to decide whether to heat or cool our houses. These thermostats can learn our daily routines, allowing them to control the temperature more efficiently than classical programmable thermostats. Furthermore, since the thermostats are connected to the internet, homeowners are able to remotely control their home temperature from their mobile phone.
AWS IoT provides application developers a protocol, Message Queue Telemetry Transport (MQTT), for communication between Internet-connected things and the cloud. Sensors use MQTT to publish data to a message broker, which passes on the sensor readings to subscribing smart appliances and other devices. These messages are also processed by a rules engine, allowing developers to interface with other AWS services, such as their storage and data processing solutions.
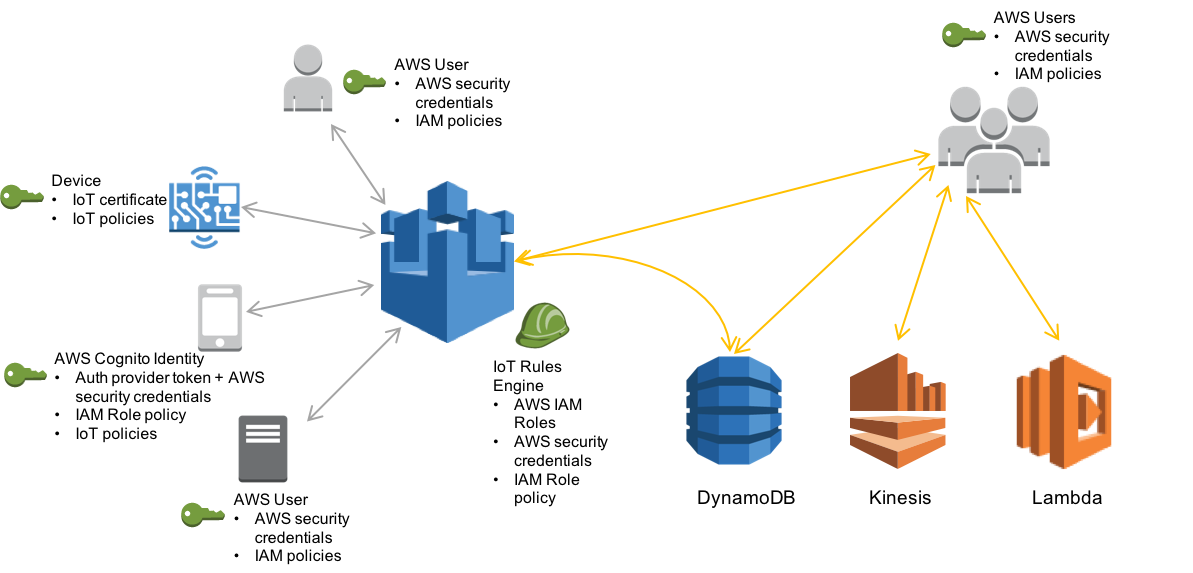
Source: Amazon
All these messages to and from AWS IoT need to be secured. To ensure privacy, TLS is used to encrypt all MQTT traffic between devices and the message broker. Devices are authenticated using one of three identity types. First, clients can use the standard X.509 certificates used in HTTPS, which are authenticated using challenge-response TLS Client Authentication. AWS IoT also allows clients to use two AWS-specific identity types: IAM roles, and Amazon Cognito Federated Identities.
Even after a device has authenticated itself to the message broker, it is only allowed to execute an operation if it has been given the appropriate permission. An entity’s permissions are specified by AWS IoT policies, which are attached to the entity’s identity (certificate, IAM role, or Cognito identity). If an entity needs access to AWS services outside of IoT, IAM policies are used instead of IoT policies. These policies provide developers fine-grained control of authorization.
AWS End-To-End Hardware Security
Brandom Lewis. AWS, Microchip deliver trust anchor for end-to-end IoT security. Embedded Computing Design, 7 October, 2016.
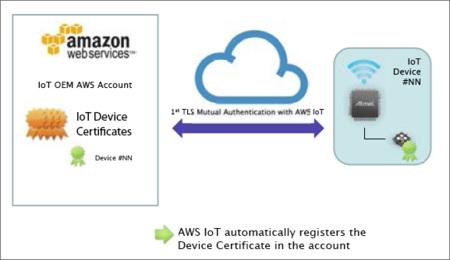
Digital certificates are ingrained in almost every aspect of our digital lives. Signed by Certificate authorities (CAs), they help authenticate the identity of parties involved in the electronic exchange of information, preventing potential threats such as MITM attacks. With the Internet of Things (IoT) introducing billions of clients that communicate with the cloud in a two-way fashion, the requirement for mutual authentication of both clients and servers has steadily increased nowadays.
To solve the problems related to certificate provisioning for client-side devices, Amazon Web Services (AWS) released “Use Your Own Certificate” feature this April. It allows original equipment manufacturers (OEMs) to register digital certificates signed by a third-party CA with the AWS IoT platform using an API, which, could happen even before the devices come online. This provides a new possibility for OEMs to generate cryptographic keys for device during its production period. The latest capability in the AWS IoT portfolio, Just-In-Time Registration (JITR), is also partly based on such process. As the term implies, devices can automatically connect to and be recognized by the AWS IoT cloud the first time they request service from the platform. By ensuring them being pre-equipped with unique, trusted private keys and correct server configurations and policies, such immediate, autonomous onboarding of devices with cloud services can maintain secure despite the large numbers of connections.
Fortunately, good news have arrived from hardware side of IoT spectrum as well. One example is ECC508A, a 2 mm x 3 mm tamper-resistant CryptoAuthentication device based on elliptic curve Diffie-Hellman (ECDH) algorithms. The architectural features of the chip include internally encrypted memory, isolated power rails, a memory and logic shield, internal clock generation, and a lack of probe points to protect against different kinds of real-world threats. It also improves overall system performance when TLS transaction runs on hardware-based crypto accelerator. With the ECC508A acting as the root of trust, Microchip can act as a third-party CA, signing device certificates in an offline verification process. Then OEMs are able to access robust security and automatic cloud authentication by adding a single component to their bill of materials (BoM).
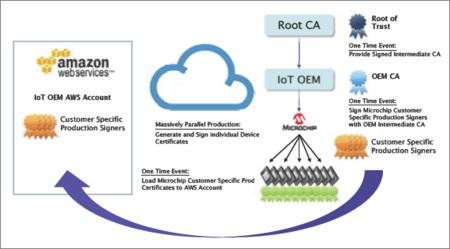
Security is still essential to the continued rollout of IoT in every market. Device makers now can separate security from business functions and continue to work upon that. The ECC508A evaluation kit has been available on the market, which must excite those who deeply concern and care about the future of cyber security.
Conclusion
As we have seen, TLS is being widely used outside of the web in embedded devices, the Internet of Things, Amazon Web Services, and many others. The problem, however, is how these devices choose to implement their own versions of TLS and the problems that ensue. We have seen interesting applications of TLS that seem to also fundamentally break the intended security inherent in the protocol. Many of the problems are actually just based on laziness in the production of these devices, such as pinning a single certificate to every type of a device.
Besides TLS, alternative protocols have been designed for minimal data use and enhanced security throughout all communication between these devices. Because of the limited resources provided by embedded devices and IoT devices, many of the protocols must consider how much CPU, battery, and memory will be used at a time.
As time goes on, more and more of these embedded devices will be in our homes and cities, and there is the very real possibility of our own physical safety being in harm’s way due to a compromised device. Internet enabled doors, heating systems, windows, safes, and more could hold the potential of being locked, overused, and unlocked to cause danger to their owner. While TLS never was designed with the idea outside of web use, we must begin to consider alternative protocols or improve current ones to ensure the security of our technology outside of our browsers.
TLS Evolves: Version 1.3
TLS v1.3 is a major revision to TLS to simplify the protocol, and improve its security and performance. In order to get a good understanding of TLS v1.3 and where it is heading in the future, we will first look at where TLS has been.
Looking Backward: Retro TLS
SSL/TLS has a storied past. SSL v1.0 was never released. Netscape, the company that originally developed SSL, circulated it internally but decided not to release it to the public because it had several flaws including a lack of data integrity protection.
After that non-starter, the timeline looks like this:
- 1994: Netscape develops SSL v2.0 which is shipped with the Netscape Navigator 1.1
- 1995: SSL v2.0 has serious security issues; Netscape releases SSL v3.
- 1999: TLS v1.0 released; standardizing and upgrading SSL v3.0
- 2006: TLS v1.1 released; address the BEAST attack, which will come in 5 years
- 2008: TLS v1.2 released with Authenticated Encryption
- 2011: Google deploys public key pinning and forward secrecy
- 2013: Work on TLS v1.3 begins
A more thorough timeline can be found at SSL/TLS and PKI History.
So what does TLS v1.3 bring to the table? Let’s take a look…
Faster Handshake
TLS 1.3 introduces a significantly slimmer Handshake Protocol than previous versions. In order to understand the implications of these changes, we first review the Handshake Protocol used in TLS 1.2.
In TLS 1.2, the client begins the handshake with a Client Hello,
followed by a Server Hello response from the server. The client then
proceeds with a Client Key Exchange and Client Finished; the
server responds with its own versions of these messages.
In contrast, TLS 1.3 incorporates the key share messages with the
Client/Server Hello, meaning that each side of the connection has to
send one less message (and only send one message total to initiate the
connection).
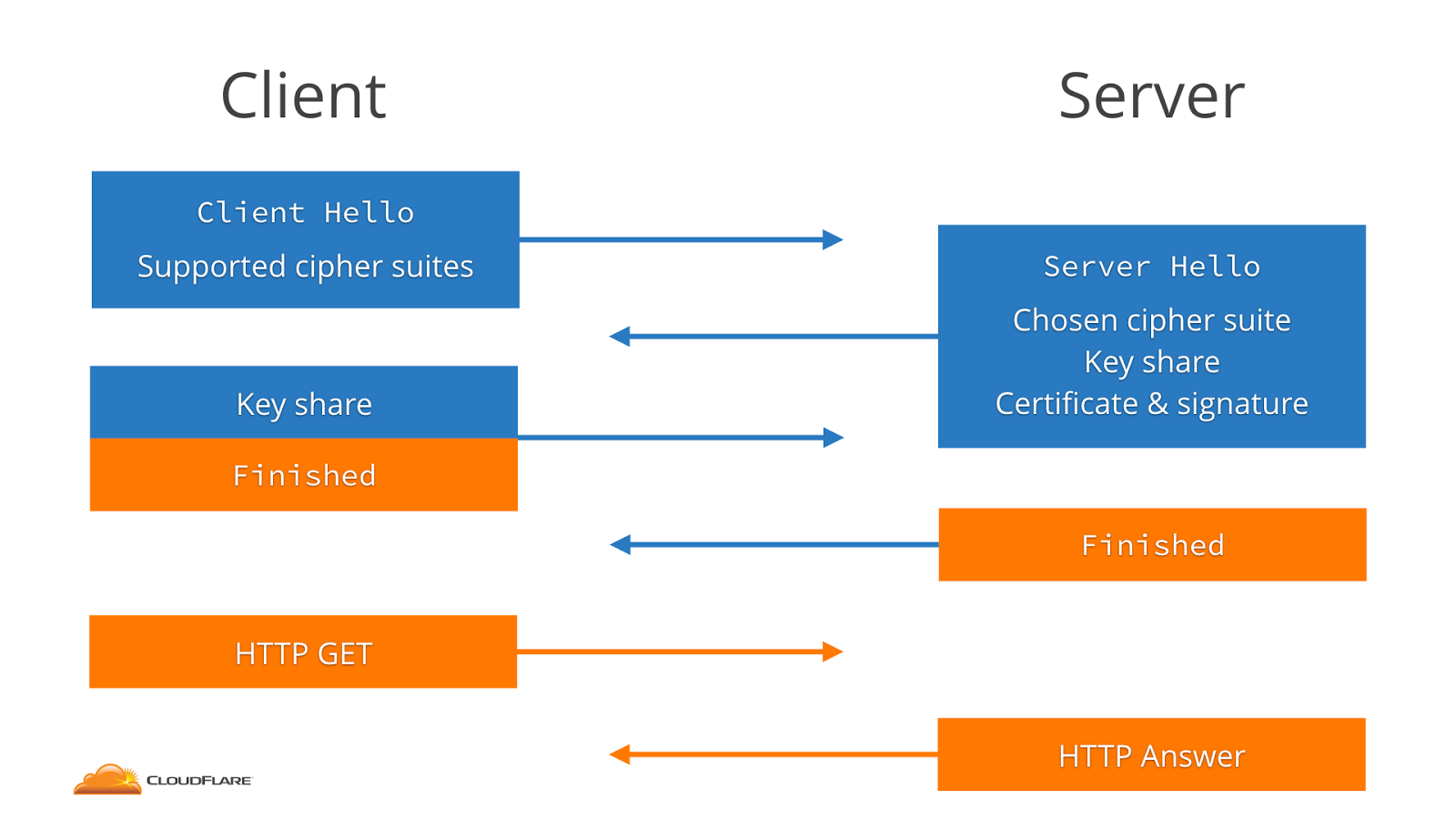
TLS 1.2 Handshake
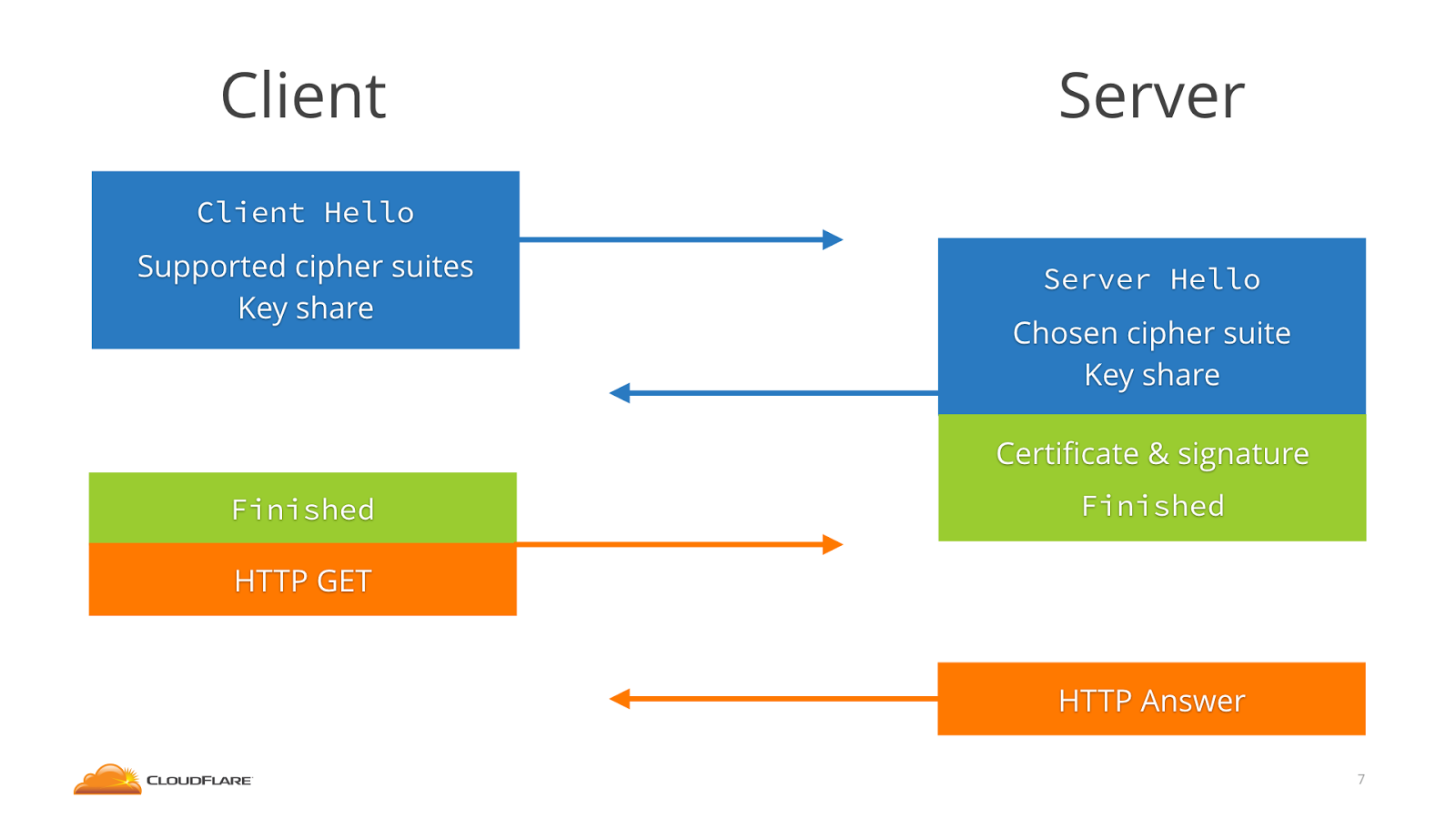
TLS 1.3 Handshake
Sidebar: AuthLoop
AuthLoop: End-to-End Cryptographic Authentication for Telephony over Voice Channels, Bradley Reaves, Logan Blue, and Patrick Traynor. USENIX Security Symposium. August 2016.
On the subject of modification and adaptations to the typical TLS 1.2 system of encryption and authentication, we explore AuthLoop: a TLS-style authentication protocol specifically designed for telephony networks. In this domain, the system must connect three different types of telephony networks: cellular, VoIP, and PSTN. However, the TLS Handshake transmission speeds for such a system were extremely slow - averaging 98 seconds per handshake - which is completely infeasible for most phone calls. AuthLoop keeps the authentication and shared secret elements of TLS and a freshness/liveness component analogous to the Heartbeat Protocol. On the other hand, AuthLoop removes RSA and the cipher agreement messages. Furthermore, AuthLoop does not encrypt messages and therefore has no Record Protocol. After slimming down, the average transmission time reduced drastically to 4.8 seconds.
0-RTT Resumption
A major new feature in the TLS 1.3 draft is support for 0-RTT session resumption. In TLS 1.2, establishing a connection to a new server required at least 4 trips between the server and client to make an HTTP request and receive a response. With a session-ID or session ticket, that could be reduced to 3 trips per connection. TLS 1.3 by default reduces the number for new connections to only 3 trips per connection, but also adds support for a new mode termed 0-RTT. In this mode, resumed HTTPS connections require only 2 trips, which is the bare minimum required for a full HTTP query and response. In this mode, TLS 1.3 adds barely any additional latency cost over a plain HTTP request!
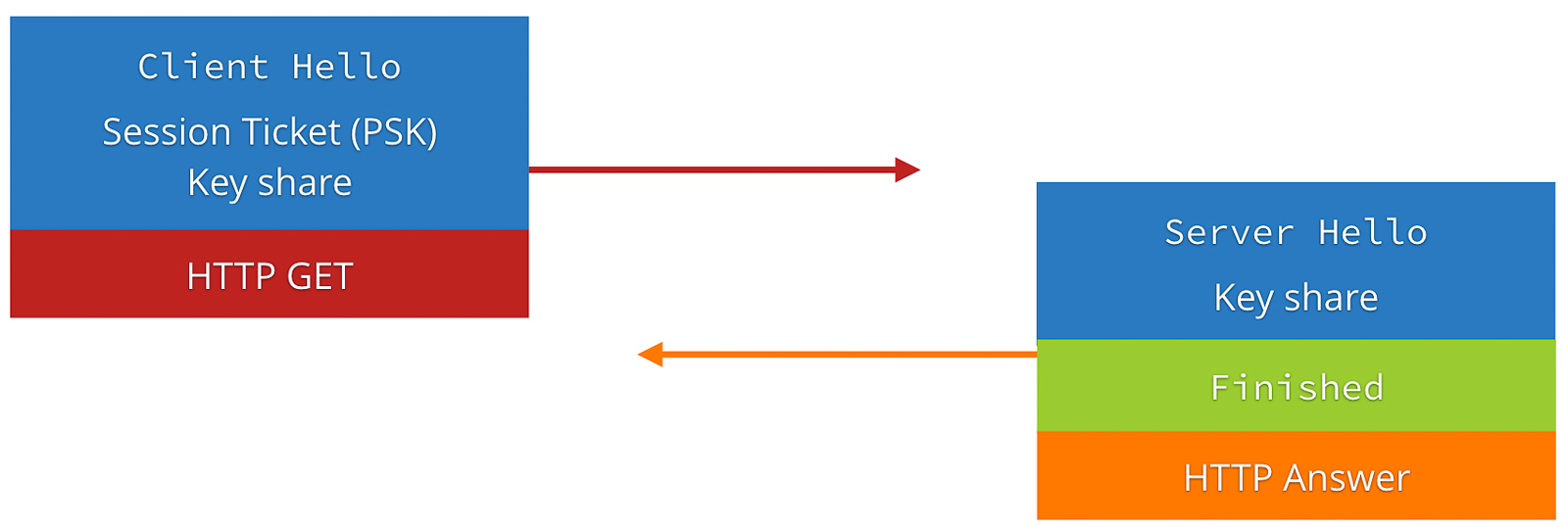
TLS 1.3 0-RTT (Source: https://blog.cloudflare.com/tls-1-3-overview-and-q-and-a/)
However, the addition of 0-RTT resumption to the protocol has an important implication for the security features provided by the protocol. Because TLS 1.3 session tickets, which enable 0-RTT resumption, are stateless on the server, such requests from the client are trivially vulnerable to replay attacks. An attacker who can intercept an encrypted client message can re-send it to the server, tricking the server into processing the same request twice (which could be serious, for example, if the request is “transfer $x to Bob”).
To remedy this, the protocol authors recommend that initial requests from the client be idempotent, or non-state-changing. Servers should not allow the first request to be idempotent in 0-RTT mode. This has been arguably the most controversial part of the new standard, as it puts the onus on some higher level protocol to solve a problem that TLS has historically been responsible for. Even worse, it is not solved directly by HTTP but rather must be specifically kept in mind by web developers.
Deployment
Deployment of TLS 1.3 remains loosely in the future as the protocol specification finishes its final draft. Current TLS 1.3 drafts include 0-RTT by requiring servers to set up a profile that defines its use. However, as with many other features in earlier TLS protocols, 0-RTT data is not compatible with older servers. A server using TLS 1.3 has the option to limit what early data to use in a 0-RTT and what to buffer.
Data Center use of Static Diffie-Hellman: While ephemeral (EC) Diffie-Hellman is in nearly all ways an improvement over the TLS RSA handshake, it has a limitation in certain enterprise settings. Specifically, the use of ephemeral (PFS) ciphersuites is not compatible with enterprise network monitoring tools such as Intrusion Detection Systems (IDS) that must passively monitor intranet TLS connections made to endpoints under the enterprise’s control. Such monitoring is ubiquitous and indispensable in some industries, and loss of this capability may slow adoption of TLS 1.3.
Deployment of TLS 1.3 across the web faces several industry concerns, most notably regarding Static RSA (no forward secrecy), as posted from an email exchange between Andrew Kennedy, an employee at BITS (the technology policy division of the Financial Services Roundtable http://www.fsroundtable.org/bits), and Kenny Paterson.
Andrew Kennedy writes,
… While I am aware and on the whole supportive of the significant contributions to internet security this important working group has made in the last few years I recently learned of a proposed change that would affect many of my organization’s member institutions: the deprecation of RSA key exchange.
Deprecation of the RSA key exchange in TLS 1.3 will cause significant problems for financial institutions, almost all of whom are running TLS internally and have significant, security-critical investments in out-of-band TLS decryption.
Like many enterprises, financial institutions depend upon the ability to decrypt TLS traffic to implement data loss protection, intrusion detection and prevention, malware detection, packet capture and analysis, and DDoS mitigation.
Kenny’s response: (excerpted from https://www.ietf.org/mail-archive/web/tls/current/msg21278.html)
Hi Andrew,
My view concerning your request: no.
Rationale: We’re trying to build a more secure internet.
Meta-level comment:
You’re a bit late to the party. We’re metaphorically speaking at the stage of emptying the ash trays and hunting for the not quite empty beer cans.
More exactly, we are at draft 15 and RSA key transport disappeared from the spec about a dozen drafts ago. I know the banking industry is usually a bit slow off the mark, but this takes the biscuit.
Cheers,
Kenny
Anti-Downgrade Prevention and Detection
Downgrade resilience in key-exchange protocols by Karthikeyan Bhargavan, Christina Brzuska, Cédric Fournet, Markulf Kohlweiss, Santiago Zanella-Béguelin and Matthew Green in IEEE Symposium on Security and Privacy (SP), 2016.
TLS 1.2 suffers from various downgrade and man-in-the-middle attacks like Logjam, FREAK and POODLE. Logjam exploits the option of using legacy “export-grade” 512-bit Diffie–Hellman groups in TLS 1.2. It forces susceptible servers to downgrade to cryptographically weak 512 bit Diffie-Hellman groups, which could then be compromised. FREAK is a man-in-the-middle attack that affects the OpenSSL stack, the default Android web browser, and some Safari browsers. It tricks servers into negotiating a TLS connection using cryptographically weak 512 bit encryption keys. POODLE exploits vulnerability in SSL 3.0 but is applicable to TLS 1.2 once the attacker performs version rollback to SSL 3.0 through a man-in-the-middle attack.
The above problems can be countered using correct downgrade protection. While TLS 1.2 does implement downgrade protection, it fails to do so correctly. Downgrade protection requires sending MAC of finished messages between client and server to ensure that the negotiated parameters have not be modified by a MITM attacker. TLS 1.2 does not hash all the negotiated parameters in its MAC allowing the attacker to alter the non-hashed parameters and launch downgrade attacks. TLS 1.3 fixes this issue by hashing all the parameters and also isolates TLS 1.2 or lower version messages (which have downgrade resilience issues) by requiring the TLS 1.3 server to set first N bits of its ServerRandom nonce to a fixed value on recieving ClientHello message from a TLS 1.2 or below client. This signals the TLS 1.3 clients and they reject any packet that has the fixed value sequence.
Downgrade Resilience in Key-Exchange Protocols
Downgrade protection primarily relies on the MACs in the finished messages, which in turn rely on the strength of the group and the negotiated algorithms and hash. If a client and server support a weak group, then an attacker can downgrade the group and break the master secret to forget the MACs, as in Logjam.
The figure below shows the faulty downgrade resilience of TLS 1.2, where the TLS 1.2 server fails to hash the negotiated parameters like protocol version (v), chosen parameters (a_R) and server identity (pk_R) in its hash message hash_1(.) (see subfigure (b) of the below figure).
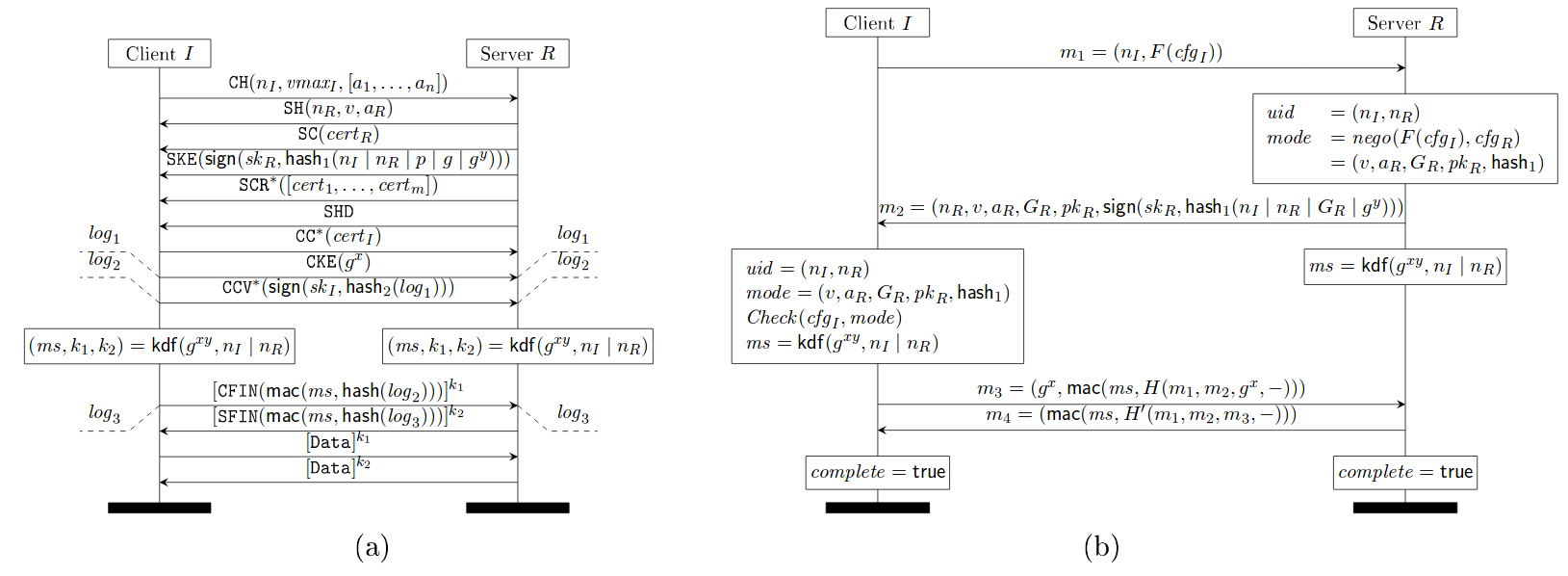
TLS 1.0 - 1.2 with (EC)DHE key exchange (a), where messages labeled with * occur only when client authentication is enabled, and (b) its downgrade protection sub-protocol
Source: https://eprint.iacr.org/2016/072.pdf
Draft 10 of TLS 1.3 implements the following downgrade protection mechanism which rectifies the above mistake and consequently hashes all the negotiated parameters. Notice the hash_1(H(m_1, m_2, -)) in the message sent by server (subfigure (b) in the figure below), which hashes all the negotiated parameters in m_2.
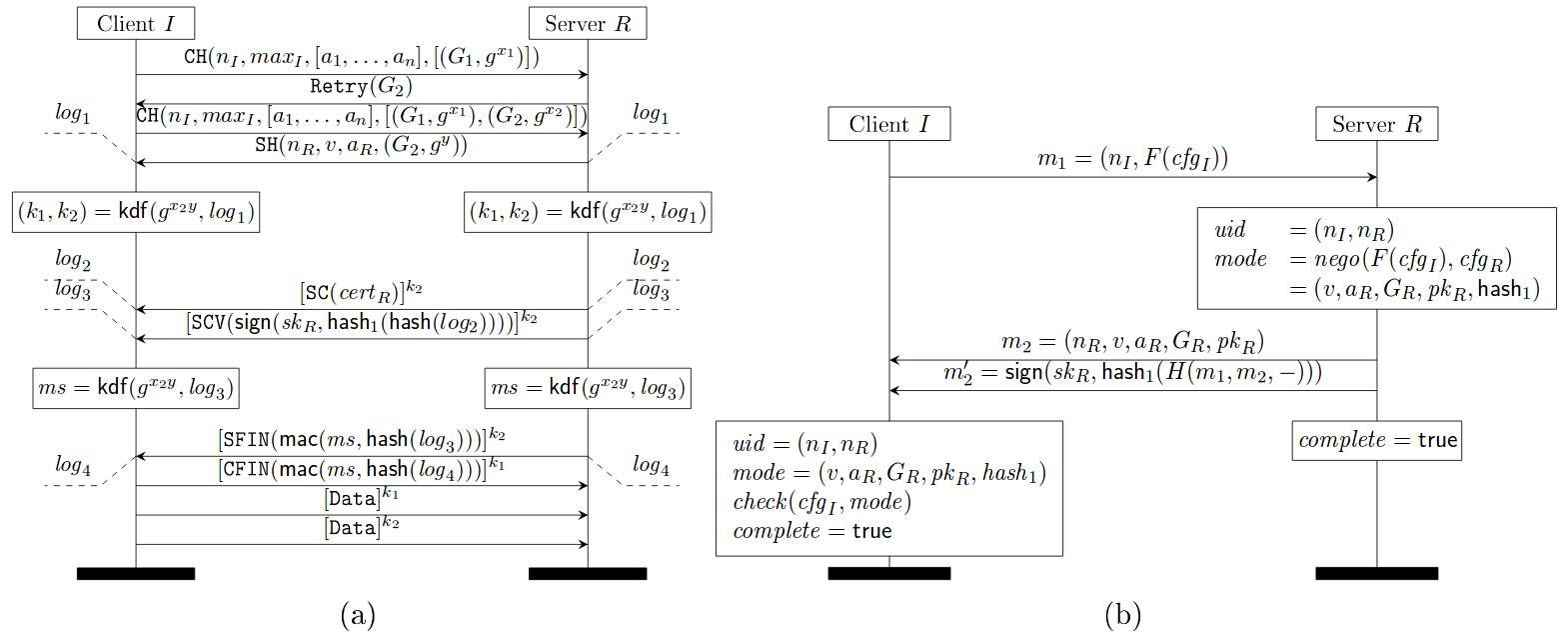
TLS 1.3 1-RTT mode with server-only authentication (a) and its downgrade protection sub-protocol (b)
Source: https://eprint.iacr.org/2016/072.pdf
However, there are three downgrade attacks possible on TLS 1.3 as described in Draft 10. One, an attacker downgrades the connection to TLS 1.2 or lower and mounts any of the downgrade attacks mentioned before. This will succeed as long as the attacker can forge the finished MACs. Second, an attacker uses the TLS fallback mechanism to stop TLS 1.3 connections and allows only TLS 1.2 connections to go through. Even if the end points implement the fallback protection mechanism, the attacker can use one of the downgrade attacks in TLS 1.2 to break the connection. Third, in Draft 10 of the TLS1.3 protocol, the handshake hashes restart upon receiving a Retry message and hence, the attacker can downgrade the Diffie-Hellman group for some classes of negotiation functions.
TLS 1.3 draft 11 counters the above three attacks by incorporating two countermeasures.
First, TLS 1.3 protocol continues the handshake hashes over retries (subfigure (a) of the figure below).
Second, TLS 1.3 servers always include their highest supported version number in the server nonce, even when they choose a lower version such as TLS 1.0.
Draft 11 of TLS 1.3 fixed the issue by requiring TLS 1.3 server to set top N bits of the ServerRandom to be a specific fixed value on receiving ClientHello message from a TLS 1.2 or below client. TLS 1.3 clients which receive a TLS 1.2 or below ServerHello check for this value and abort if they receive it. The figure below shows the client check using verifyVersion functionality.
This allows for detection of downgrade attacks over and above the Finished handshake as long as ephemeral cipher suites are used. This prevents attacks targeted at (EC)DHE.
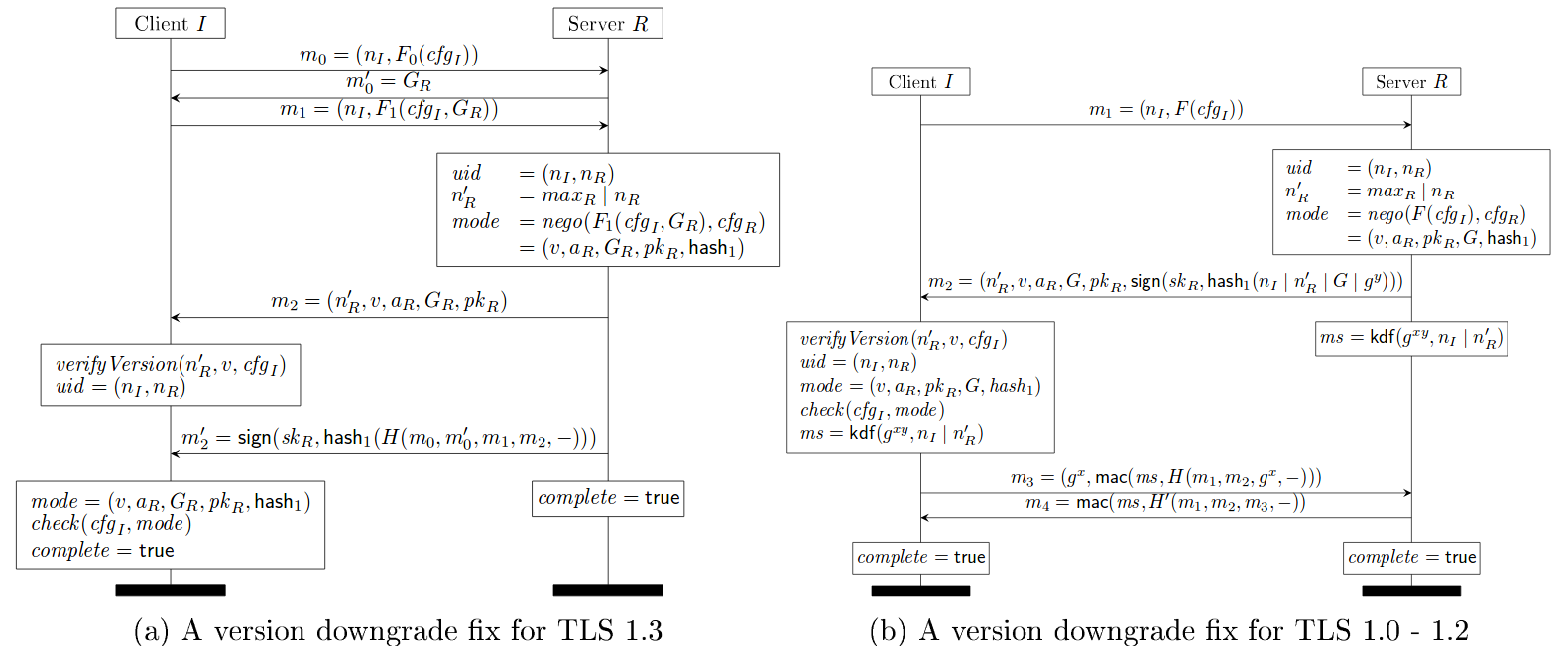
TLS 1.3 Draft 11 Update on Downgrade Resilience in Key-Exchange Protocols
Source: https://eprint.iacr.org/2016/072.pdf
The TLS 1.3 server will send a ServerHello message in response to a ClientHello message when it is able to find an acceptable set of algorithms and the client’s key_share extension is acceptable. If it is not able to find an acceptable set of parameters, the server will respond with a handshake_failure fatal alert. The ServerHello message contains server’s random value which incorporates downgrade protection mechanism. If a ClientHello indicates only support for TLS 1.2 or below, then the last eight bytes of server’s random value MUST be set to: 44 4F 57 4E 47 52 44 01.
If a ClientHello indicates only support for TLS 1.1 or below, then the last eight bytes of server’s random value SHOULD be set to: 44 4F 57 4E 47 52 44 00.
TLS 1.3 clients are required to check the above values in the random field of server responses.
Authenticated Encryption
Up until now, we’ve mostly concerned ourselves with the “MAC-Encode-Encrypt” (MEE) packet construction method. In a nutshell, MEE follows three steps:
- Calculate a MAC over the payload
- Append the MAC and an appropriate amount of padding to the payload
- Encrypt the modified payload to generate a ciphertext
As we’ve discussed in previous classes, the CBC mode of operation has its downsides; adversaries can break encryption by utilizing padding oracle attacks, since padding can only exist in a handful of values and lengths. Moreover, it’s impossible to actually verify the integrity of the ciphertext until the MAC has been revealed by decrypting the ciphertext. The duration required to decrypt the tampered ciphertext and validate the MAC leaks sensitive (and potentially useful) timing information to adversaries.
Encrypt-then-MAC
In general, MEE is inferior to its cousin, “Encrypt-then-MAC” (ETM). In ETM, as opposed to MEE, the plaintext is encrypted before the MAC is calculated. Intuitively, it makes sense that ETM is more secure—any tampering of the ciphertext is immediately evident when the MAC is calculated, therefore no decryption takes place (and no timing information is leaked). Additionally, assuming the ciphertext appears random, the MAC also appears random and reveals no information about the underlying ciphertext.
Galois/Counter Mode (GCM)
Before we jump on the ETM bandwagon, however, let’s take a look at yet another mode of operation, Galois/Counter Mode (GCM). GCM is an authenticated encryption algorithm that provides confidentiality and integrity, and does so extremely efficiently.
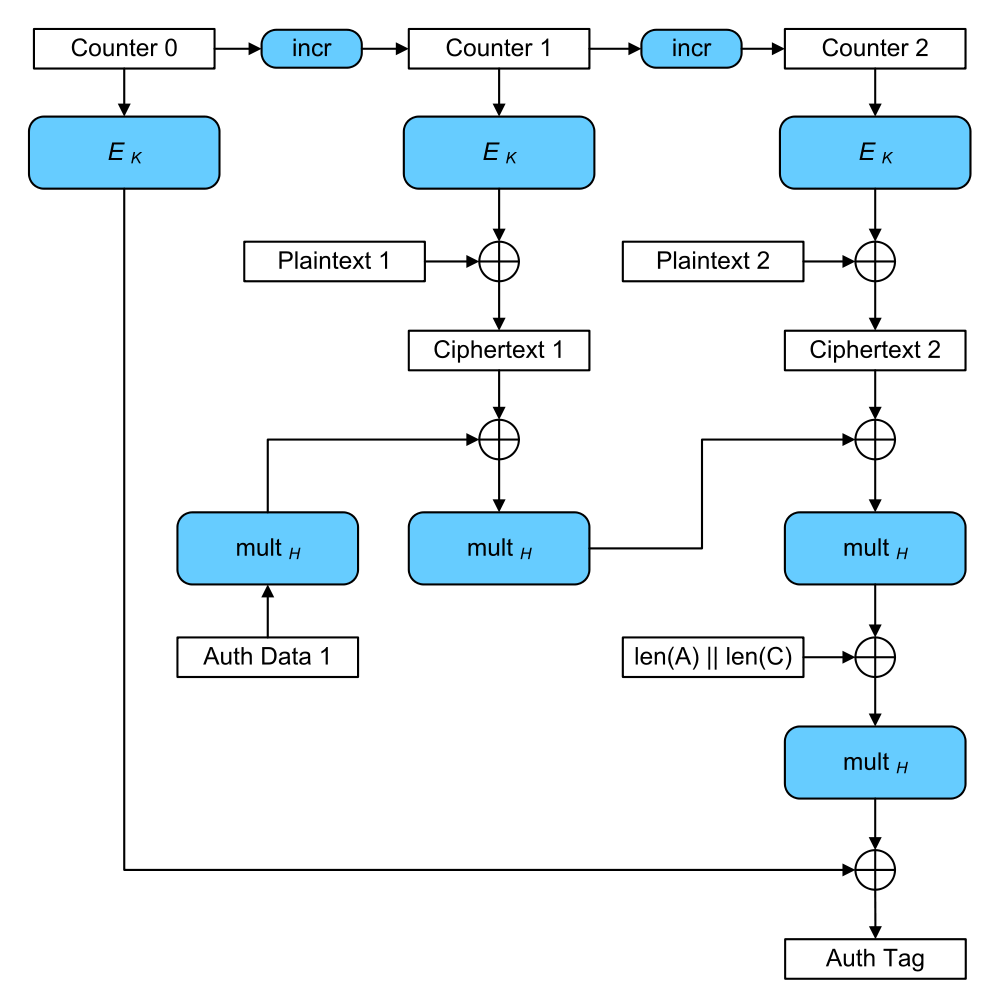
Galois/Counter Mode (credit: Wikipedia)
GCM At-A-Glance
- Sequentially number blocks
- Encrypt block numbers with block cipher E
- XOR result of encryption with plaintext to produce ciphertext
- Combine ciphertext with authentication code to produce authentication tag
The authentication tag can be used to verify the integrity of the data upon decryption, similar to an HMAC. If this “counter mode” of authenticated encryption seems superior, that’s because it is! TLS 1.3 only provides support for GCM, CCM, and ChaCha20-Poly1305, another authenticated encryption mode of operation. Say goodbye to MAC-then-encrypt.
TLS v1.3 Removals
An overview of TLS 1.3 and Q&A
In TLS v1.3, everything was scrutinized for being really necessary and secure, and scrapped otherwise. In particular, the following things are removed:
- static RSA handshake
- the CBC MAC-then-Encrypt modes, which were responsible for Vaudenay, Lucky13, POODLE, LuckyMinus20
- weak primitives like RC4, SHA1, MD5
- compression
- renegotiation
- custom FFDHE groups
- RSA PKCS#1v1.5
- explicit nonces
Formal Verification
TLS 1.3 is the first revision of the TLS protocol to incorporate formal verification during development. Cas Cremers, Marko Horvat, Sam Scott, and Thyla van der Merwe’s paper, Automated Analysis of TLS 1.3: 0-RTT, Resumption and Delayed Authentication, provides a recent (February 2016) description of the challenges and results of such an analysis. In the blog post associated with their work, the authors contextualize their verification efforts:
The various flaws identified in TLS 1.2 and below, be they implementation- or specification-based, have prompted the TLS Working Group to adopt an “analysis-before-deployment” design paradigm in drafting the next version of the protocol. After a development process of many months, the TLS 1.3 specification is nearly complete. In the spirit of contributing towards this new design philosophy, we model the TLS 1.3 specification using the Tamarin prover, a tool for the automated analysis of security protocols.
The authors are able to prove that revision 10 of the specification meets the goals of authenticated key exchange for any combination of unilaterally or mutually authenticated handshakes. Further, the authors discovered a new, unknown attack on the protocol during a PSK-resumption handshake. The 11th revision of the protocol included a fix for this attack.
Protocol Model
The authors used the Tamarin prover for their analysis. Tamarin is an interactive theorem proving environment (similar to Coq) specially designed for the verification of protocols such as TLS. As TLS is already an abstract specification, encoding TLS 1.3 into the Tamarin specification language was relatively straightforward. “Rules” (functions) over this specification captured honest-party and adversary actions alike. The following state diagram depicts the client TLS state (as defined in Tamarin) and transitions between the states (Tamarin rules) for an entire session.
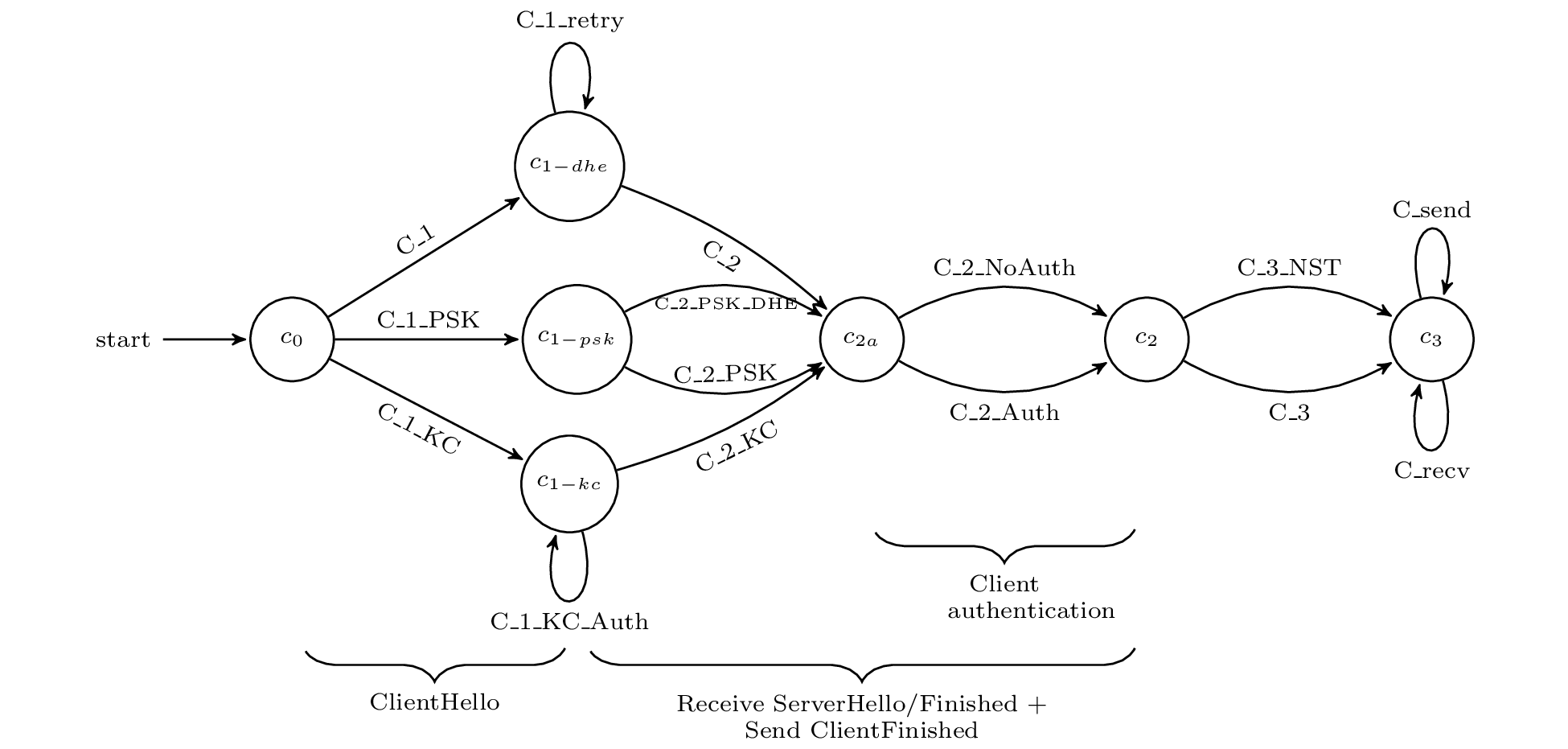
Source: Automated Analysis of TLS 1.3
Proven Security Properties
The next step in the analysis involved encoding the desired security properties of TLS 1.3 as Tamarin lemmas. The authors encoded the following properties:
- unilateral authentication of the server (mandatory)
- mutual authentication (optional)
- confidentiality and perfect forward secrecy of session keys
- integrity of handshake messages
Each lemma must hold over its respective domain of states (a subset of the nodes in the client state machine above, for example). While proof assistants like Tamarin are capable of constructing simple proofs, a significant amount of manual effort was required to prove the enumerated lemmas. As such, a notable contribution of this work is the actual Tamarin proof artifact itself, not just what was and wasn’t proven. The authors claim their Tamarin abstractions and proofs were constructed with extensibility to future TLS development in mind.
Discovered Attack
While verifying the delayed authentication mechanism portion of the protocol, an attack was discovered which violated client authentication; an adversary is able to impersonate a client while communicating with the server.
Step 1. The victim client, Alice, establishes a connection with the man-in-the-middle attacker, Charlie. Charlie establishes a connection with Bob, the server which which Alice wishes to connect. A PSK is established for both connections, PSK_1 and PSK_2, respectively.

Source: Automated Analysis of TLS 1.3
Step 2. Alice sends a random nonce, nc, to Charlie using PSK_1. Charlie reuses this nonce to initiate a PSK-resumption handshake with Bob. Bob responds with random nonce ns and the server Finished message using PSK_2. Charlie reuses ns and recomputes the Finished message for Alice using PSK_1. Alice Returns her Finished message to Charlie. Charlie then recomputes this Finished message for Bob using PSK_2.

Source: Automated Analysis of TLS 1.3
Step 3. Charlie makes a request to Bob that requires client authentication. Charlie is thus prompted for his certificate and verification. This request is re-encrypted and forwarded to Alice. To compute the verification signature of this forwarded request, Alice uses the session_hash value, which is the hash of all handshake messages excluding the Finished messages. This session_hash value will match that of Charlie and Bob’s, and thus Charlie can re-encrypt Alice’s signature for Bob. Bob accepts Alice’s certificate and verification as valid authentication for Charlie.

Source: Automated Analysis of TLS 1.3
The discovery of this attack is noteworthy in that it was completely unexpected by the TLS Working Group.
The fix, which forces the session_hash value to include Finished messages was even suggested in an official pull request, but was rejected.
The authors make a strong case that formal verification has been an extremely valuable part of the design process of TLS 1.3. The speed with which the fix was incorporated into subsequent protocol revisions suggests that the TLS Working Group shares this sentiment.
Two Oakland 2017 papers provide more reports on formal verification efforts for TLS 1.3, up through Draft 18:
- Karthikeyan Bhargavan, Bruno Blanchet, and Nadim Kobeissi. Verified Models and Reference Implementations for the TLS 1.3 Standard Candidate. IEEE Symposium on Security and Privacy, May 2017.
- Karthikeyan Bhargavan, Antoine Delignat-Lavaud, Cédric Fournet, Markulf Kohlweiss, Jianyang Pan, Jonathan Protzenko, Aseem Rastogi, Nikhil Swamy, Santiago Zanella-Béguelin, and Jean Karim Zinzindohoué. Implementing and Proving the TLS 1.3 Record Layer. IEEE Symposium on Security and Privacy, May 2017.
Introduction
In 1999, Alma Whitten and Doug Tygar performed a usability analysis of PGP 5.0 called Why Johnny Can’t Encrypt. PGP Corp claimed its product “makes complex mathematical cryptography accessible for novice computer users”.
However, Whitten and Tygar’s evaluation, based on experiments with users, argued that PGP’s user interface design made computer security usable only for people who are “already knowledgeable in that area”. This does not seem to be a fair expectation for users. Today, around 40% of the entire world population use the internet. When the paper was published, that percentage was 4.1%. Thus, as the number of internet users has skyrocketed, the security community has become increasingly aware of how important it is to make security understandable and accessible to typical users.
Usability is, of course, important for any service that is a vital part of the lives of billions. However, for security in particular, there are higher stakes— confusing user interfaces can lead to sensitive data being exposed, from financial transactions to identification information. HTTPS users are vulnerable to significant, real-life risks when technical language abounds and browsers inundate them with too many warnings (many of which are false positives).
Humans are arguably the weakest link, so usability and communication must be taken into account in any model that expects the user to act safely. When a user interface fails to effectively communicate security consequences, it is unreasonable to blame an improperly informed user for exposing themselves to those dangers.
Users Are Not The Enemy
Users Are Not The Enemy, Anne Adams and Martina Angela Sasse. Communications of the ACM. December 1999.
Even perfectly written software can become vulnerable to attacks when the user does not understand its behavior. In Users Are Not the Enemy, Adams and Sasse discuss how users can both knowingly and unknowingly compromise computer security mechanisms such as password authentication. In authentication, few users knew how to or even understood the need to constitute a secure password. As a result, most of the passwords revolved around familiar and related phrases, words, or character patterns. Because the average person finds it difficult to remember passwords, most users rarely change the passwords and some prefer to record them in plaintext.
Users are the reason, however, not the true enemy. Without sufficient knowledge of hacking techniques, typical users understandably default to their own models of security threats and priorities. Meanwhile, security experts and developers do not always understand the users’ perceptions, tasks, or needs. Before quickly dismissing users as unknowing collaborators in cyberspace crime, we should educate them in why we are protecting their account. Consequently, they would be more motivated to practice security-conscious behaviors when they perceive a threat.
The Source Awakens
The Source Awakens. Presentation at USENIX Enigma 2016 by Matthew Smith.
We often see breaking news articles detailing the most recent hacking or the most recent password leak. These aren’t attacks focusing on specific users typically uneducated in cybersecurity principles but rather on firms’ products, that have been developed by computer scientists and engineers who are supposed to be experts in their fields. Now, if these developers are making mistakes, is it their lack of developing ability or is it their lack of understanding of the security issues? Considering the two, it’s best to assume the latter, as it is more likely. Therefore, developers are themselves making mistakes when they are not aware of the security issues latent in their system.
A story, which probably hits home for many software developers, is trying to Google an approach or solution to their problem or feature that they want to implement. The developer clicks on the first StackOverflow link and gets a solution, implements it, and keeps it as long as it apparently works. The developer now continues and goes about completing the task with no question to the validity of the code just implemented. What the developer doesn’t realize is that the code found and used may have serious security, such as this this code for self-signed certificate validation:
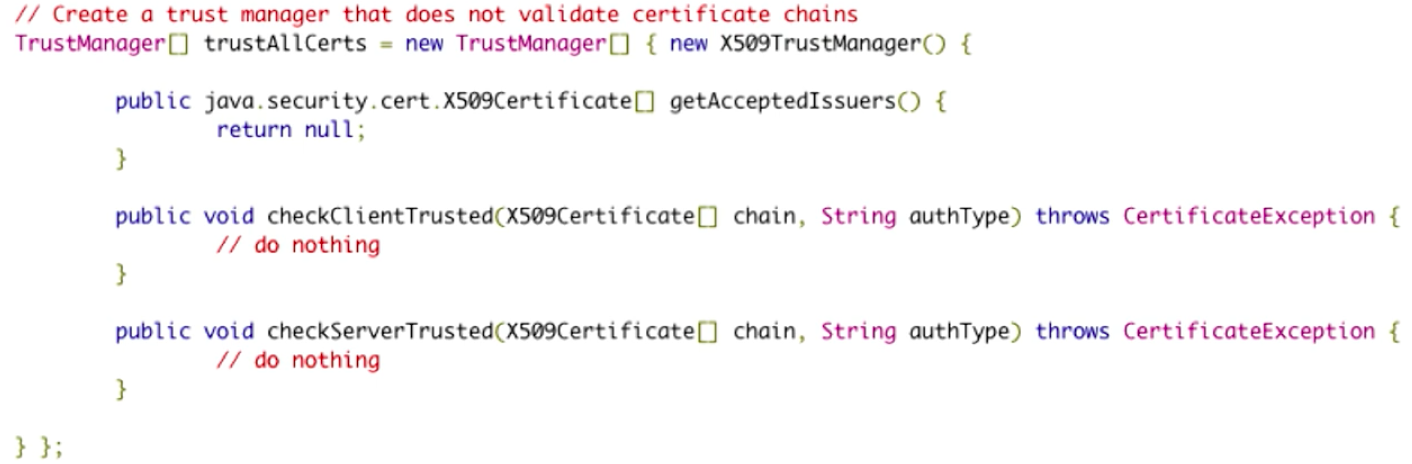
Source: The Source Awakens
The code seems to work. But, upon closer inspection, it clearly doesn’t do anything to check certificates. When this program sees any and all certificates, it simply approves every single one, regardless of what is contained within. So, of course the code “works” when the developer incorporates into their program (at least it gives no apparent errors), but it presents a major security vulnerability. Similarly, developers may use some dummy certificate validator or self-signed certificates for testing, but then forget to remove them in the release.
Thus, usability is a security issue for developers using APIs and libraries, not just for end users using graphical interfaces.
Malware Analysis Tools
There are several decompilers that take binary code and output the decompiled code, such as HexRays (shown below). But, the generated code isn’t very readable to the average programmer, such as this example from the Simda malware domain generation code:
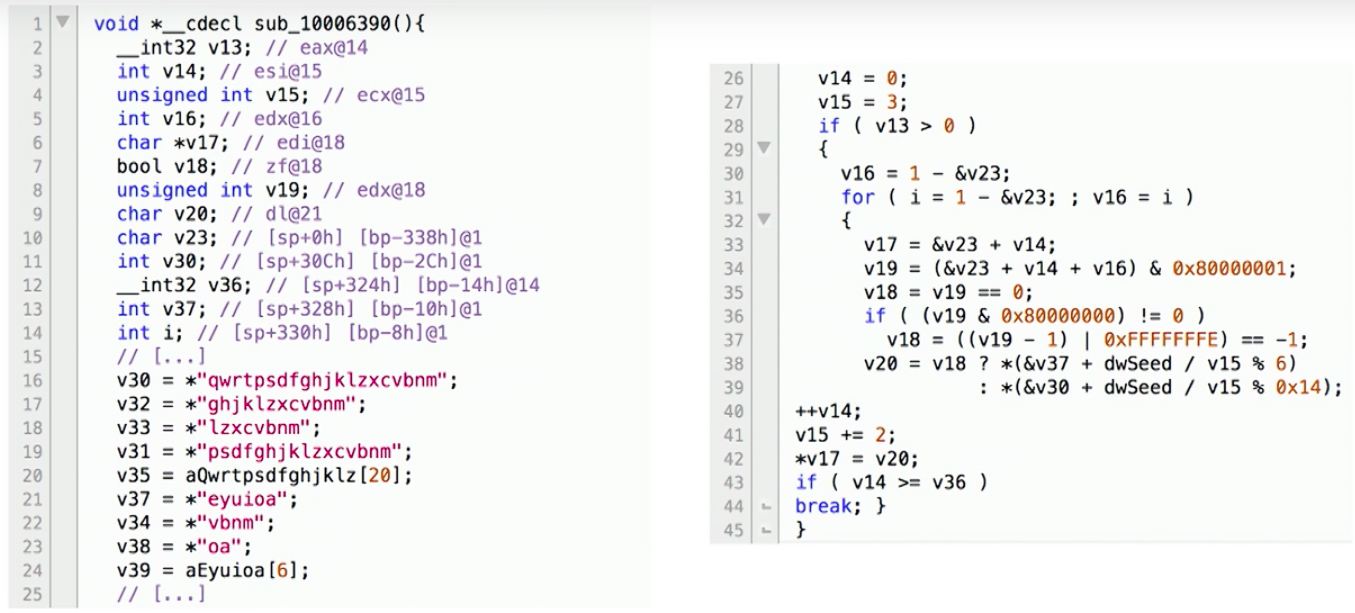
Source: The Source Awakens
Smith discusses how his team created a new system called DREAM++ that can outputs more readable decompiled code, so we may get something like:

Source: The Source Awakens
By producing more readable decompiled code, both security experts as well as typical programmers were able to much more easily and quickly understand the decompiled programs.
Browser Warnings
Improving SSL Warnings: Comprehension and Adherence by Adrienne Porter Felt, Alex Ainslie, Robert Reeder, et Al. ACM Conference on Human Factors in Computing (CHI), 2015.
Security experts and programmers will always attempt to do what is best for their end-users, but the problem is that (very) often the end-user will circumvent any attempt at stopping whatever they intend to do. Looking at HTTPS specifically, the inherent security boils down to the end user’s choice of whether or not to proceed to a possibly unsafe webpage.
Therefore, it is the web browser’s responsibility to provide adequate notice to a user when their connection is not secure. Research conducted in 2015 by Google and the University of Pennsylvania found that reducing technical jargon in Chrome browser SSL warning and focusing on brevity and simplicity, resulted in an increase in comprehension of SSL warnings. Still, only 49% of the respondent’s could answer the following question correctly:
What might happen if you ignored this error while checking your email?
Your computer might get malware
A hacker might read your email
(Technically both are true, but realistically the user is supposed to understand that invalid HTTPS results in hackers being able to read your communications in plaintext)
The researchers also found that the improved design of browser warnings could influence up to 30% more users to go “Back to Safety” rather than “Proceed to Unsafe”. The new design is shown below:
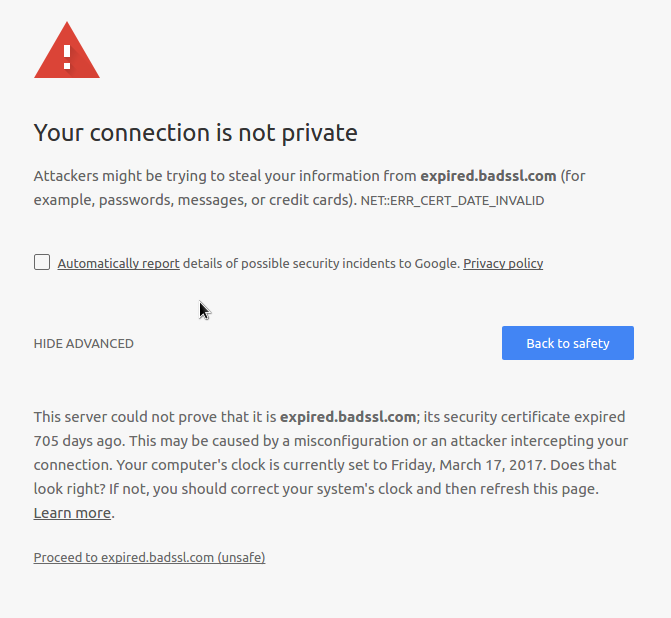
Source: Improving SSL Warnings: Comprehension and Adherence
If this seems familiar, it is because it was introduced in Chrome 37. This new design requires an extra click from a user to proceed to the potentially unsafe site. Notice that the unsafe option is a dark gray text link contrasted with a safe blue button.
Below, a blast from the past: SSL warnings from pre-2015 Chrome versions.
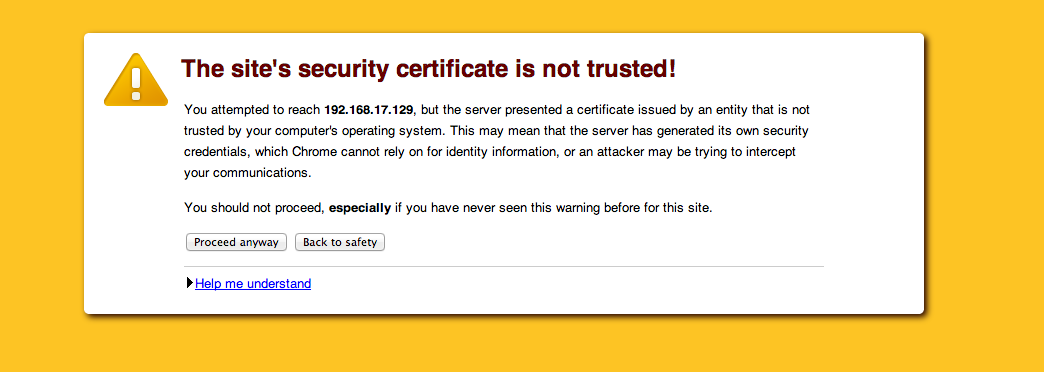
Source: Self Signed Certificates with Postman
Noticeably, this has ‘too much’ technical jargon and is neither short nor simple. Similarly the user can easily proceed to the site straight from the warning. Google’s research was meant to improve the user experience when seeing these warning to minimize the security risks taken by the end-user.
TLS Errors on the Web
Here’s My Cert, So Trust Me, Maybe? Understanding TLS Errors on the Web by Devdatta Akhawe, Bernhard Amann, Matthias Vallentin, & Robin Sommer. International World Wide Web Conference (WWW) 2013.
The end-user isn’t the only source of security issues when it comes to browser usability in TLS. The behavior of web browsers may not be studied as much as vulnerabilities in TLS, but it is almost just as dangerous in measure. Usually when browsers report TLS errors, they don’t offer distinguishing features between real attacks and benign errors; hence leaving the decision to the end-user of whether continuing is itself a security issue. On most occasions, errors will turn out to be “false positives”, which can include errors due to server misconfiguration, self-signed certificates (as mentioned previously), and name validation errors. As a result, end-users quickly train themselves to click through these warnings, regardless of the content, making it unlikely that they will pay enough attention when a real attack comes along.
This paper reports on a large-scale measurement study of common TLS warnings. A total of 11.5 billion SSL connections on all ports were captured over a nine-month period in their experiment. The warnings and errors produced were then categorized based on where they occurred during the verification: chain building errors, chain validation errors, and name validation errors. These correspond to the three separate steps of certificate validation of the Network Security Services (NSS) library, used by Firefox (and Chrome on Linux). The following is an algorithm that can translate the NSS responses into their categorization:
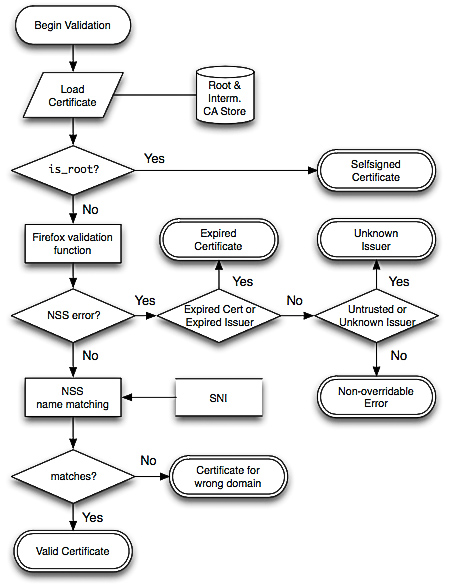
Source: Here’s My Cert, So Trust Me, Maybe?
The results of this experiment indicate a clear opportunity, and need, for reducing false warnings. A 1.54% false warning rate is unacceptable if we understand that benign scenarios are orders of magnitude more common than actual attacks.
Based on this analysis, a number of concrete recommendations are proposed to help browser vendors lower the risk of such unwanted habituation. For example, advocating the use of free TLS certificates via authorities like StartCom, using a more relaxed name validation algorithm that accepts multiple levels for an asterisk, or enabling AIA support or preload all known intermediate authorities in the browser cache. By implementing these changes, the complete usability of browsers for end-users will be significantly improved, therefore leading to a drastic decrease in attacks and security issues caused by users.
Rethinking Connection Security Indicators
Rethinking Connection Security Indicators by Adrienne Porter Felt, Robert Reeder, Alex Ainslie, Helen Harris, Max Walker, Christopher Thompson, Mustafa Emre Acer, Elisabeth Morant, and Sunny Consolvo. Twelfth Symposium on Usable Privacy and Security (SOUPS), July 2016.
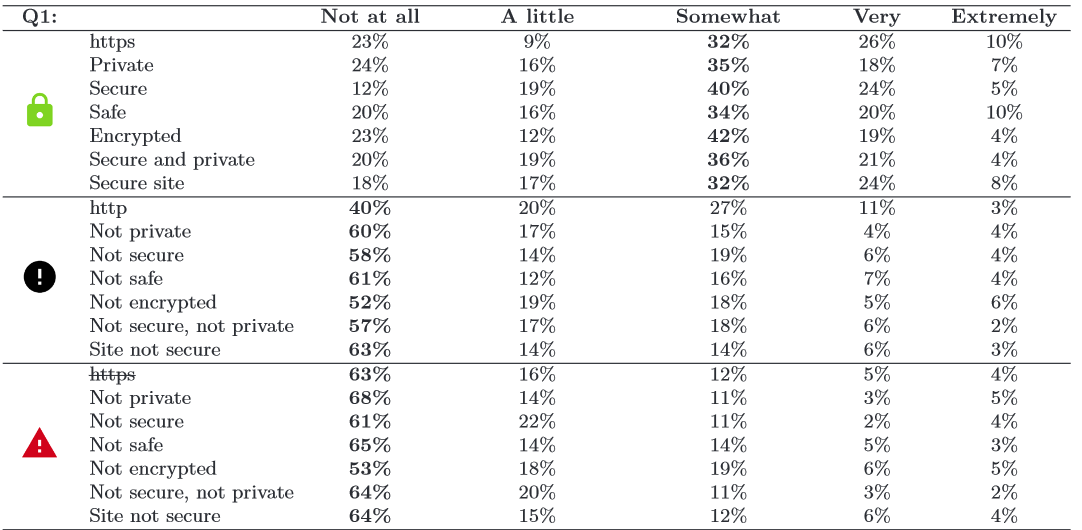
By seriously considering the ramifications of the symbology we use to send messages to the users, we can work to develop more useful and informative messages. This section focused on the findings of a study conducted to figure out how users react to various symbols appearing in their browsers (most often in the URL field). The study found that a surprising number of users could identify one or more of the significant features in a good connection, but the majority of users could not identify issues with a bad connection or one not using HTTPS.
Only about 40% of the people in the study were able to identify an HTTP connection as insecure or what protocol was being used; many of the participants believed the symbol had to do with the favicon of the page or that the symbol included general information about the page such as permissions. A summary of the results of this research can be seen in the table below.
Source: Rethinking Connection Security Indicators
The researchers attempted to identify the three symbols that would be the most effective for conveying information to the user. They then conducted more research regarding how users would interpret these symbols.
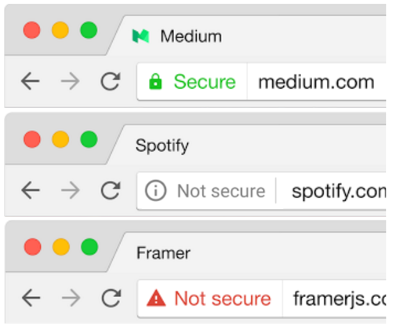
Source: Rethinking Connection Security Indicators
Source: Rethinking Connection Security Indicators
The researchers were able to confidently determine that any sign of an error is interpreted to be essentially the same, regardless of color or shape. Secondly, they determined that even if users were shown to be on https or ‘secure’ sites, they still had a ‘healthy level of paranoia’ in only being ‘somewhat’ confident in the security of the site that they were currently accessing.
Based on these results, browsers need to start asking what dangers on the internet are. Is it worse to have a fault in one’s implementation of their certificates or to not have HTTPS connection at all? Browsers can also consider blacklists of sites that are known for putting user’s information or connections at risk. Browsers could also do more to put security in a more central or significant location, such as having a pop-up before every page with information on the connection type and associated risks. We need to become more aware of what messages we’re sending to the users via the particular symbols that we choose for varying types of connections.
Conclusion
We’ve covered several studies showing progress, and the need for more research, in the area of usable security. Despite the work done to bridge the gap between experts and users, there is a still a gulf between each group’s understanding of the other. In some cases, browser designers assume that users know what a certificate is, while users assume that the green lock in their URL bar indicates a website is free of malware.
The philosophical debate between informing users more effectively and simply manipulating them to make “correct” decisions is also unresolved. The major browsers have adopted a hybrid approach with TLS error warnings that both provide basic information on the error and require significant user effort to circumvent.
Such error warnings are commonplace, which raises another issue. Users tend to become accustomed to error messages (habituation), assuming them to be false positives for genuine threats, because they actually are false positives in the vast majority of cases. Benign server administration errors account for essentially all TLS warnings that users see. Browser manufacturers are engaged in efforts to reduce the amount of noise users experience while sifting through warnings of potential hazards.
Work at the intersection of security and human-computer interaction continues to progress, but more needs to be done to ensure the security of future internet users. We can’t eliminate people, the weakest links in the chain, so we must remember design systems around their fallibility. While security is always at the forefront of most security researchers brains, we must also begin to consider the users who will be interacting with these features as a part of the system itself.
TLS Interception and SSL Inspection
The fact that “SSL inspection” is a phrase that exists, should be a blazing red flag that what you think SSL is doing for you is fundamentally broken. Compounding the problem are the mistakes that SSL inspection software authors are making.
– Will Dormann (2015), Carnegie Melon Software Engineering Institute CERT/CC Blog
Recent History
TLS Interception, also referred to as SSL Inspection, is a topic that has been in the news in recent years and months. Back in 2014, researchers from Brigham Young University published a paper titled TLS Proxies: Friend or Foe? where they deployed a Flash application via Google Adwords campaign to identify client-server certificate mismatches across the web. They discovered a wide prevalence of adware, malware and TLS proxy products presenting certificates trusted by the client but not issued by the server – and in most instances acting in a negligent manner by introducing security vulnerabilities. One parental filter they tested replaced untrusted certificates with trusted ones, bypassing browser warning screens. This is exactly the type of passive attack HTTPS aims to prevent.
Vulnerabilities involving two advertising injectors, one of which was preinstalled on Lenovo PCs, were found to severely compromise the security of end users in February of 2015. Later that same year, German journalist Hanno Böck looked at three popular antivirus suites and found that all lowered security by either exposing end users to vulnerabilities like FREAK and CRIME or supporting less secure encrpytion algorithms.
In early 2017 researchers teamed up with Google, Mozilla, and Cloudflare for an internet-wide survey - The Security Impact of HTTPS Interception ( Zakir Durumeric, Zane Ma, Drew Springall, Richard Barnes, Nick Sullivan, Elie Bursztein, Michael Bailey, J. Alex Halderman, Vern Paxson; in NDSS 2017). TLS interception software was assessed based on how the TLS connection observed from the client differed from the TLS parameters advertised by the client. In all but two of the tested products, security was reduced, and in some cases serious vulnerabilities were introduced. Most recently in February of 2017, a Chrome 56 update took down almost a third of Montgomery County Public School’s 50,000 fleet of Chromebooks offline, because the school systems web filter, BlueCoat Proxy, did not properly handle TLS 1.3. When Chrome attempted to connect via TLS 1.3, the Bluecoat software abruptly terminated the connection, rather than negotiating for TLS 1.2.
How SSL/TLS interception works
SSL/TLS interception is performed by software on “middleboxes” located in between the client and HTTPS website or on the client’s machine, in the case of malware, anti-virus software, and ad injectors. Middlebox software has both legitimate and illegitimate use cases including proxies or content filters, antivirus suites, content cachers, advertising injectors, and malware.
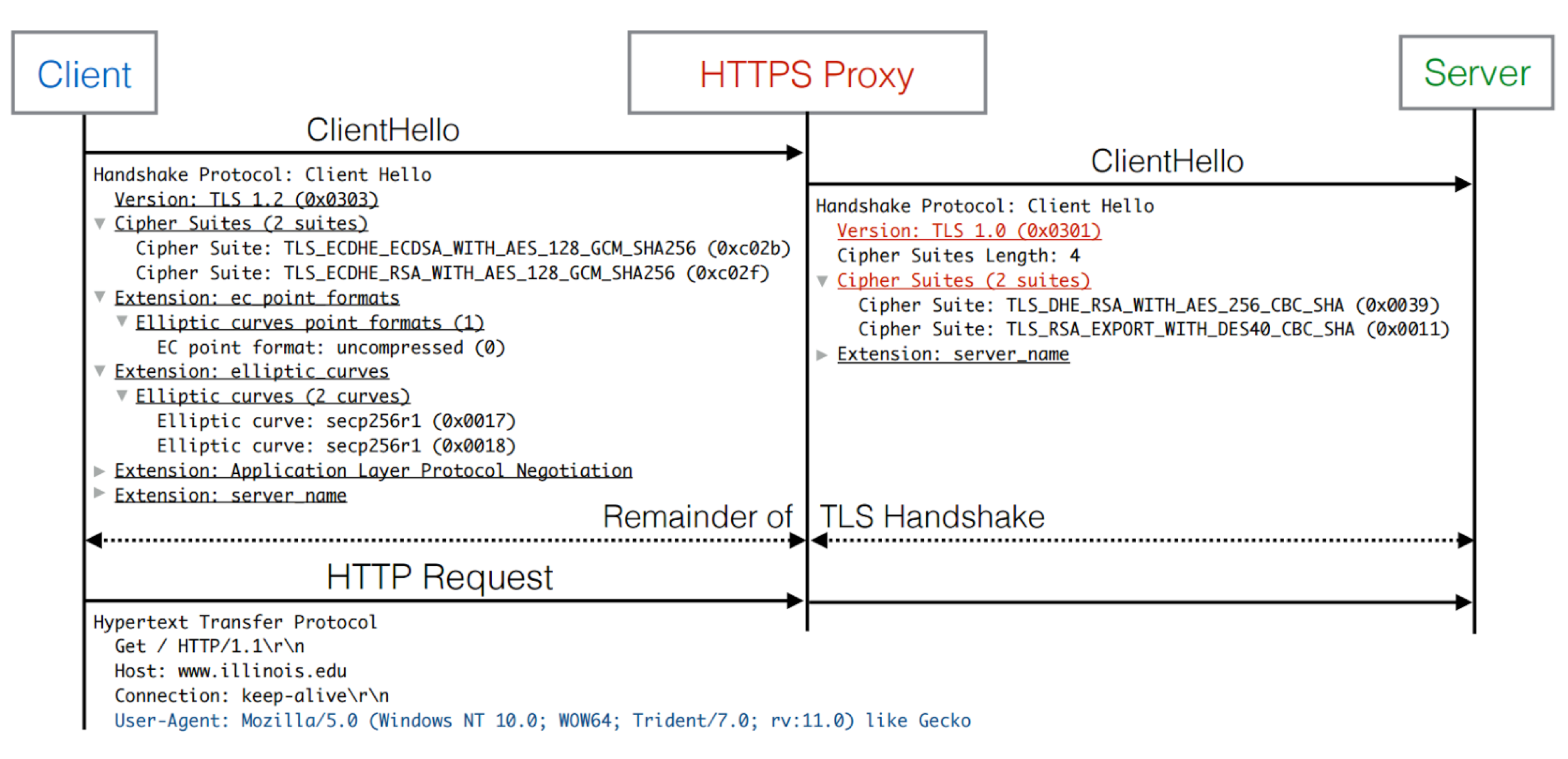
Source: The Security Impact of HTTPS Interception (2017)
Middlebox proxy software relies on the client having previously installed a root certificate onto their operating system. Any outgoing SSL/TLS connections from the client are terminated and re-established by the proxy to the server, which acts as an in-the-middle attacker. In an ideal deployment, the proxy’s ClientHello mirrors the TLS parameters expressed in client’s ClientHello, to provide the same expected parameters to the client. The proxy can then inspect plaintext and establish a TLS connection back to the client using the installed certificate to circumvent browser warnings and silently intercept the connection between client and server.
Superfish
In 2015, there was in an incident involving Lenovo PC’s shipped with a preinstalled image advertisement optimizer developed by Superfish. Superfish used Komodia’s tool “SSL hijacker” to intercept HTTPS connections in order to gather image data for its ad optimization engine. Komodia’s tool is similar to to all SSL inspectors — it first installs root certificates on the client machine and then MITMs all TLS connections to HTTPs websites, issuing the preinstalled Komodia certificate to the client instead of the target HTTPS server’s certificate to bypass browser warnings.
To enable it to generate trusted (by the browser based on the new root CA key installed) certificates for any website the user connects to, it needed to generate new certificated on-the-fly, so the private signing key for the root CA needed to be stored on the user’s device. This means that the private key for the certificate was visible in the software and could be trivially extracted by the end user. In addition, Komodia used the same private key for every machine running Superfish. It didn’t take long for security researcher Robert Grahm to crack the password for the private key (hint: it was ‘komodia’). With this key, an adversary could MITM any client running Superfish on their laptop by using using a copy of this hardcoded certificate. To compound this, users were not alerted to the presence of Superfish software on their new Lenovo laptops.
Komodia released a security notice saying they fixed the issue by updating the software to create unique certificates per installation and randomly generated passwords. They also addressed other potential vulnerabilities such as updating their list of supported cipher suites and verifying certificate revocation statuses (they support OCSP). The countermeasures outlined in their security notice serve as a starting point for all HTTPS interception software developers.
PrivDog
Shortly after the Superfish incident, another piece of TLS interception software named PrivDog made by Adtrustmedia was also found to be vulnerable. PrivDog is an advertising program which intercepts HTTPS connections and replaces “bad” advertisements with advertisements approved by Adtrustmedia.
Privdog, like the aforementioned Superfish, simply replaced certificates for a HTTPS server with new certificates signed by the root certificate they installed on the affected machine. However, the Privdog software performed no validation of the original certificate presented by the target server. Not only did it make untrusted certificates seem trusted, but legitimite websites with EV Certificates were replaced with PrivDog’s self signed certificate removing the green browser indication. Any website an affected user visited with an invalid certificate would appear valid, without browser warnings. An adversary could easily MITM a client running PrivDog by simply advertising a self-signed certificate!
The Security Impact of HTTPS Interception
The Security Impact of HTTPS Interception. Zakir Durumeric, Zane Ma, Drew Springall, Richard Barnes, Nick Sullivan, Elie Bursztein, Michael Bailey, J. Alex Halderman, Vern Paxson. Network and Distributed Systems Security Symposium (NDSS) 2017.
In early 2017, researchers teamed up with Google, Mozilla and Cloudflare in efforts to measure TLS interception in an internet wide study. They noted that TLS interception software can be detected from the server’s point of view by identifying a mismatch between popular browsers TLS handshakes and the observed handshake. Going one step further, by observing the TLS handshakes of popular interception software they were able to construct fingerprints for some of the most widely used interception products.
The study measured interception from the vantage point of the Cloudflare CDN, Firefox Update servers, and popular e-commerce sites. Important results from the study found that about 5-10% of measured HTTPS connections were intercepted, and much of the software reduced the security of the end user in one way or another, with 97%, 54%, and 32% of connections to Firefox, Cloudflare, and e-commerce sites becoming less secure respectively. Interestingly, the only middlebox software to earn a grade of ‘A’ was BlueCoat Proxy.
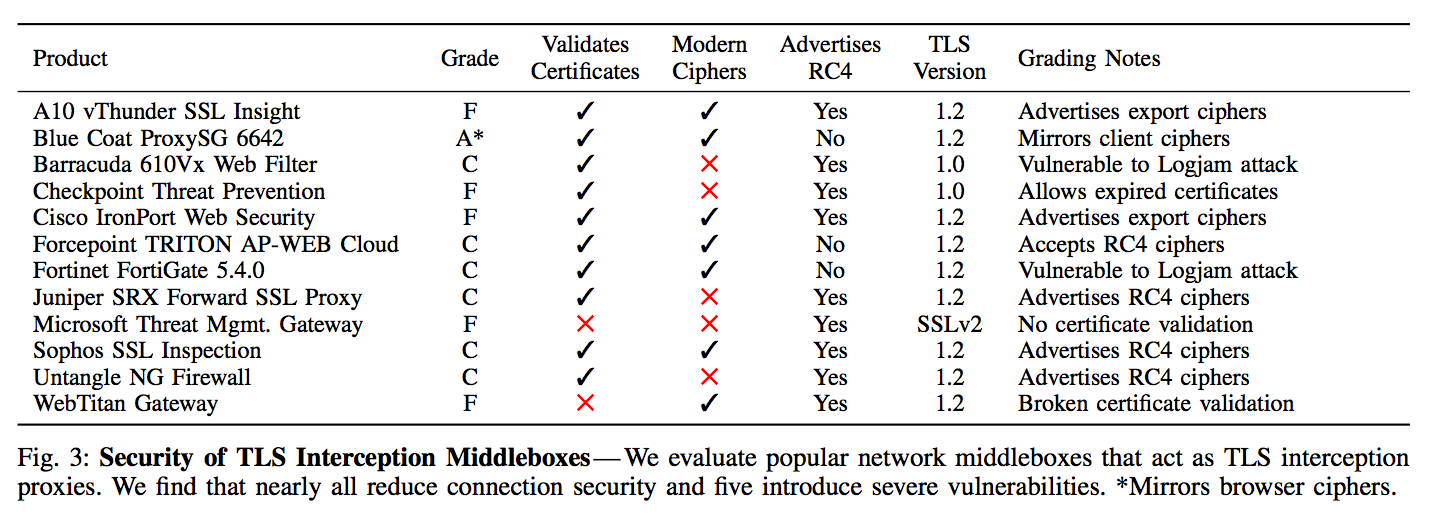
Source: The Security Impact of HTTPS Interception
Chrome 56 update breaks Bluecoat Proxy v6.5
Note these issues are always bugs in the middlebox products. TLS version negotiation is backwards compatible, so a correctly-implemented TLS-terminating proxy should not require changes to work in a TLS-1.3-capable ecosystem […] That these products broke is an indication of defects in their TLS implementations
– David Benjamin, Chromium Bug Tracker (2017)
On 21 February 2017, shortly after the above paper was published, mishandling of TLS 1.3 connections by BlueCoat Proxy left thousands of clients without internet connection after an automatic Chrome 56 update. The problem wasn’t that BlueCoat Proxy didn’t implement TLS 1.3, but that it didn’t gracefully renegotiate down to TLS 1.2 which it does support. Instead, the software simply terminated the incoming connection. This left tens of thousands of Chromebooks used by Montgomery County Public Schools students temporarily unable to connect to the internet. The temporary solution was for individual users to alter Chrome’s internal settings to disable TLS 1.3 chrome://flags/#ssl-version-max until a more general solution was delivered by the following day by Chromium, which rolled-back TLS 1.3 support by default.
Going Forward
Whether it be at the cost of availability or end user security, these incidents expose the fragility of TLS interception software. Google has reached out to middlebox vendors in efforts to help them resolve the issues, but system administrators should consider the risks of TLS interception seriously. There are, however, situations where it is necessary such as when companies are legally required to monitor traffic of their employees to comply with regulations (such as in the financial industry). Vendors should independently strive to fix their products for the security of their users at the same time. Organizations who deploy TLS interception software should choose products in an informed manner and carefully consider the risks imposed by interception software.
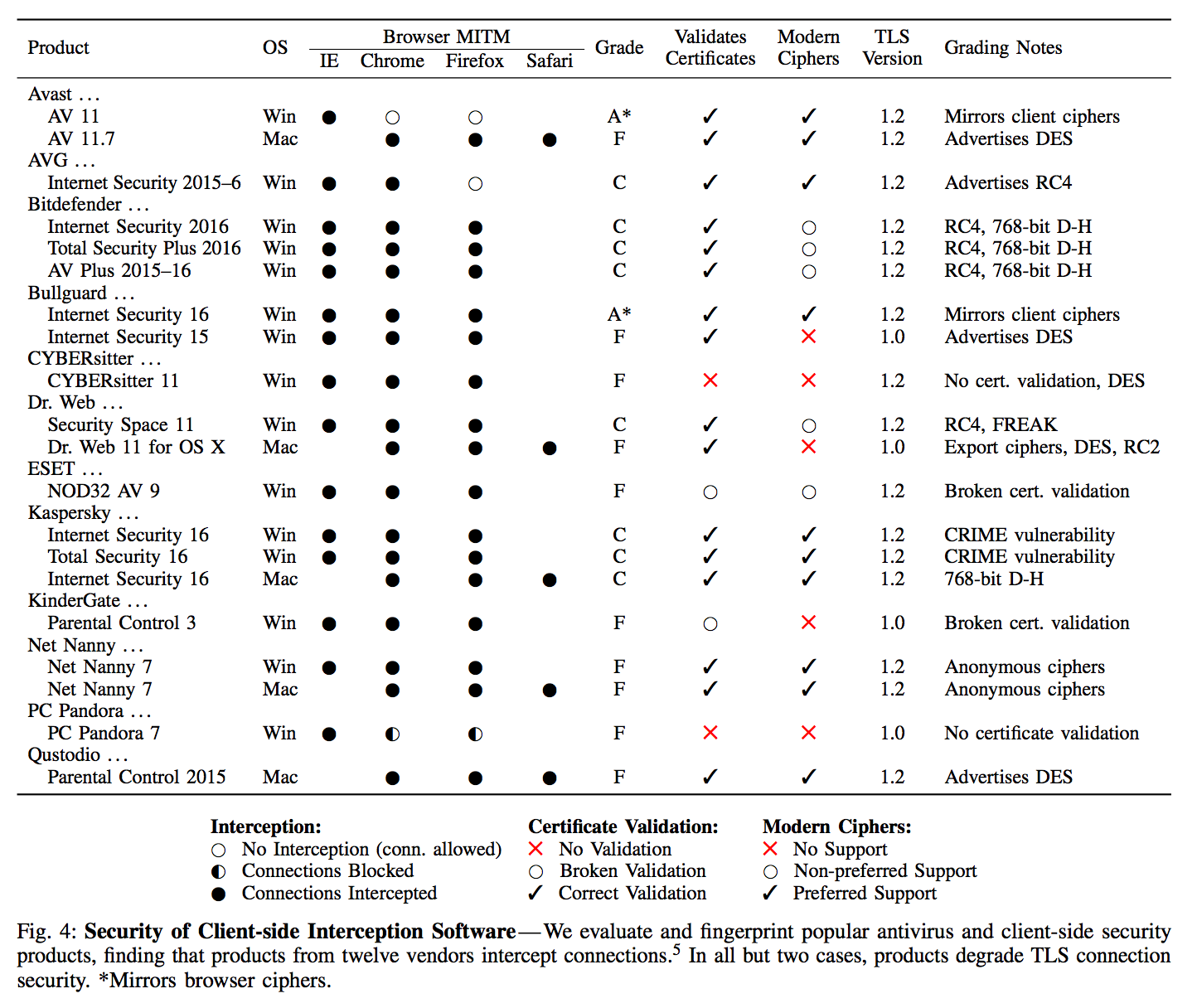
Source: The Security Impact of HTTPS Interception (2017)
I hope everyone is enjoying Spring Break!
You can see the results of the survey here: Mid-Course Survey Results (I edited one response that mentioned another student since that wasn’t intended to be public, but otherwise it is everything that was submitted.)
Based on the survey responses, and the depletion of Team Poppyseed, I have made some adjustments to the teams and schedule. Team Sesame, Team Cinnamon, and Team Poppyseed have been turned into a Smoked Salmon Shmear, and reformed as Team Pineapple (which is Team Sesame and some additions from Poppyseed) and Team Mango. Teams should wrap-up their remaining blogging responsibilities as they were (that is, Team Poppyseed is still responsible for completing the blog for Class 7, which hopefully is well underway already).
| Team Pineapple | Team Mango |
|
Adam Imeson (aei5uj) Bethlehem Naylor (bn9eb) Bhuvanesh Murali (bm4cr) Collin Berman (cmb5nh) Daniel Saha (drs5ma) Haina Li (hl3wb) Joshua Holtzman (jmh2ba) Reid Bixler (rmb3yz) Tianyi Jin (tj2cw) |
Anant Kharkar (agk7uc) Bargav Jayaraman (bj4nq) Benjamin Lowman (brl2xx) Bill Young (wty5dn) Cyrus Malekpour (cm7bv) Darion Cassel (dfc9ed) Sam Havron (sgh7cc) Yuchi Tian (yt8mn) |
I don’t want to increase the presentation and blogging workload for the rest of the semester, though, especially since I want to ensure everyone has time to work on your project. So, each team will still be leading every third week, and blogging every third week, and we will do something else in the other classes.
Team Mango is scheduled to lead the next class on March 17 (this is what was assigned to Team Cinnamon, so not a new responsibility for most of the team, and the new recruits from Team Poppyseed should have limited roles expected for this first presentation since they just joined the reformulated team). Team Pineapple is responsible for Blogging and Food for the class. Note that according to the survey results, 73.4% of the class is sick of bagels. So, Team Pineapple is challenged to come up with something more interesting for breakfast.
The full revised schedule is below. Note that the team that is not leading the class is responsible for both Blogging and Food.
| Date | Topic | Team Mango | Team Pineapple |
| Class 8 (17 Mar) | TBD | Lead | Blog, Food |
| Class 9 (24 Mar) | TBD | Blog, Food | Lead |
| Class 10 (31 Mar) | TBD | ||
| Class 11 (7 Apr) | TBD | Lead | Blog, Food |
| Class 12 (14 Apr) | TBD | Blog, Food | Lead |
| Class 13 (21 Apr) | TBD | ||
| Class 14 (28 Apr) | Mini-Conference | ||
Digression: Notable News
Two newsworthy events occurred this week that are of high importance and relevant to TLS in general: SHA-1 Collisions and the Cloudflare Leak. (Those are discussed in the separate linked posts.)
Introduction
Timing attacks exploitd information leaked from timing side-channels to learn private data. In this threat model, an attacker is able to observe the time required for certain parts of a program at runtime and gain information about the execution path followed.
Consider the following snippet of Python code as an example:
def comp(a, b):
if len(a) != len(b):
return False
for c1, c2 in zip (a, b):
if c1 != c2:
return False
return True
The comp() function performs string comparison, returning True if the strings are character-wise equal and False otherwise. Let us assume for the sake of simplicity that the lengths of the strings are public (we are not concerned with timing leaks from the initial length comparison).
Suppose we compare the strings "hello" and "catch". These words fail the string comparison immediately, since the first letters are different. Thus, the function returns False after a single iteration of the loop. In contrast, comparing "hello" with "hella" will require 5 iterations before returning False. An attacker can use the resulting timing delay to determine that "hello" and "hella" share beginning characters, whereas "hello" and "catch" do not. If "hello" was a password, an attacker who could measure the timing precisely enough to count loop iterations would be able to incrementally guess each letter of the string.
One solution to this problem would be to use a Boolean flag initialized to True. If the words have mismatched characters, the flag will be set to False, and the flag will be returned after comparing all characters. In theory, this masks the timing leak; in practice, a compiler may optimize such code to return early, reinstating the timing leak. Furthermore, there may still be timing leaks in the execution of the code, such as variation in the instruction cache depending on which statements are entered.
Thus, we see from this simple example that verifying constant-time implementation of code has many challenges, which we further discuss below.
Remote Timing Attacks are Practical
Remote timing attacks are practical. David Brumley and Dan Boneh (2005).Computer Networks, 48(5), 701-716.]
At the heart of RSA decription is a modular exponentiation \( m = c^d mod~N\) where \(N = pq\) is the RSA modulus, d is the private decryption exponent, and c is the ciphertext being decrypted. OpenSSL uses the Chinese Remainder Theorem (CRT) to perform this exponentiation. With Chinese remaindering, the function \( m = c^d mod~N\) is computed in two steps:
Evaluate \( m_1 = c^{d_1} mod~p\) and \( m_2 = c^{d_2} mod~q\) (\(d_1\) and \(d_2\) are precomputed from \(d\)).
Combine \(m_1\) and \(m_2\) using CRT to yield m.
Both steps could have timing side channels if not implemented carefully.
Chinese Remainder Theorem
Suppose that \(n_1,n_2,…,n_r\) are pairwise relatively prime positive integers, and let \(c_1,c_2,…,c_r\) be integers.
Then the system of congruences,
\(X \equiv c_2 (mod~n_2)\)
…
\(X \equiv c_r (mod~n_r)\)
has a unique solution modulo \(N = n_1n_2…n_r\)
Gauss’s Algorithm
\(X \equiv c_1N_1{N_1}^{-1} + c_2N_2{N_2}^{-1} + … + c_rN_r{N_r}^{-1}(mod~N)\), where
\(N_i{N_1}^{-1} \equiv 1 (mod~n_i)\)
Hasted’s Broadcast Attack
Hasted’s Broadcast Attack relies on cases when the public exponent \(e\) is small or when partial knowledge of the secret key is available. If \(e\) (public) is the same across different sites, the attacker can use Chinese Remainder Theorem and decrypt messages!
Hasted’s Broadcast Attack works as follows:
- Alice encrypts the same message \(M\) with three different public keys \(n_1\) \(n_2\) and \(n_3\)
, all with public exponent \(e=3\), The resulting \(C_1C_2\) and \(C_3\) are known.
\(M^3 \equiv C_1 (mod~n_1)\)
\(M^3 \equiv C_2 (mod~n_2)\)
\(M^3 \equiv C_3 (mod~n_3)\) - An attack can then recover \(M\):
\(x = C_1N_1N_1^{-1} + C_2N_2N_2^{-1} + C_3N_3N_3^{-1}~mod~n_1n_2n_3 \)
\(M = \sqrt[3]{x}\)
Montgomery Reduction
Montgomery Reduction is an algorithm that allows modular arithmetic to be performed efficiently when the modulus is large.
The reduction takes advantage of the fact that \(x~mod~2^n\) is easier to compute than \(x~mod~q\); the reduction simply strips off all but the \(n\) least significant bytes.
Steps needed for the reduction:
The Montgomery Form of \(a\) is \(aR~mod~q\), where \(R\) is some public \(2n , n\) chosen based on underlying hardware.
Multiplication of \(ab\) in Montgomery Form: \(aRbR = cR2\).
Pre-compute \(RR^{-1}~mod~q\).
Reduce: \(cR^{2}R^{-1}~mod~q = cR~mod~q\).
\(c\) can be kept in form and reused for additional multiplications during sliding windows.
To escape Montgomery space and return to \(q\) space: multiply again by \(R^{-1}\) to arrive at solution \(c\).
\(c = ab~mod~q\) (performing \(mod\) by \(q\) causes successive subtractions of \(ab\) by \(q\) till result \(c\) in range \([0,q)\). The number of “extra reductions” depends on the private data; the attack exploits these as a timing side channel.
(Image credit)
Protections against timing attacks
There are numerous defenses against timing attacks, but known defenses are either expensive or only provide partial mitigation.
Use a decryption routine with the number of operations is independent of input. For example, simply carry out the maximum number of Montgomery extra reductions, even if they are not necessary. This might be hard to mend to existing systems without replacing their entire decryption algorithm (and it is important to be wary of “overly-optimizing” compilers that remove non-functional code that is there to mask a timing leak).
By quantizing all RSA computations. This decreases performance because “all decryptions must take the maximum time of any decryption”.
By blinding, which works as follows:
- Calculate \(x = reg~mod~N\) before actual decryption for random \(r\) chosen each time
- Decrypt as normal.
- Unblind: divide by \(r~mod~N\) to obtain the decryption of the ciphertext \(g\).
Since \(r\) is random, \(x\) is also random – and input \(g\) should have minimal correlation with total decryption time.
Remote Timing Attacks are Still Practical
Timing attacks target cryptosystems and protocols that do not run in constant time. Elliptic curve based signature schemes aim at providing side-channel resistance against timing attacks. For instance, scalar multiplication is achieved via Montgomery’s ladder which performs a sequence of independent field operations on elliptic curves. Brumley and Tuveri reveal a timing attack vulnerability in OpenSSL’s implementation of Montgomery’s ladder that consequently leaks the server’s private key.
What is Montgomery’s Ladder?
Consider the right-to-left square-and-multiply algorithm to compute an exponentiation operation:
Right-to-Left Square-and-Multiply Algorithm
Source: https://cr.yp.to/bib/2003/joye-ladder.pdf
The above algorithm performs more operations when the bit is set, thereby leading to a possible timing attack. Montgomery’s power ladder method, on the other hand, performs the same number of operations in both the cases. This prevents timing based side-channel attacks as well as makes the algorithm more efficient by making it parallelizable. The algorithm is as below:

Montgomery’s Ladder
Source: https://cr.yp.to/bib/2003/joye-ladder.pdf
OpenSSL’s implementation of Montgomery’s Ladder
OpenSSL uses Elliptic Curve Cryptography for generating Digital Signatures to sign a TLS server’s RSA key. Elliptic Curve Cryptography for Digital Signature uses the following curve for binary fields:
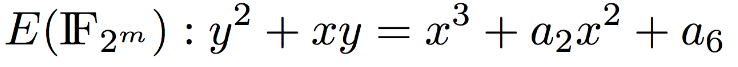
Parties select private key as \(0 < d < n\) and public key as \([d]G\) and then proceed to generate digital signatures using elliptic curves as:
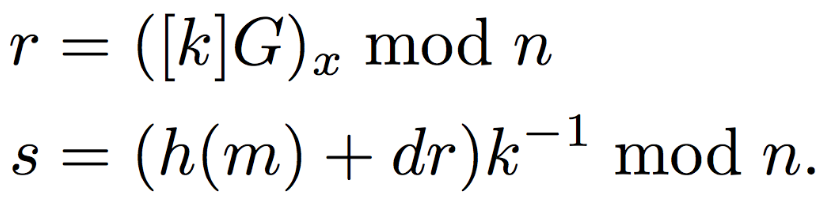
OpenSSL uses Montogmery’s ladder to compute the above digital signatures since it requires multiple exponentiation operations. However, OpenSSL’s implementation has a flaw that leads to timing attack. Below is OpenSSL’s implementation:

OpenSSL’s implementation of Montgomery’s Ladder
Source: https://gnunet.org/sites/default/files/Brumley%20%26%20Tuveri%20-%20Timing%20Attacks.pdf
Countermeasure
A possible countermeasure as proposed by Brumley and Tuveri is to pad the scalar \(k\):
Countermeasure to OpenSSL’s flaw
Source: https://gnunet.org/sites/default/files/Brumley%20%26%20Tuveri%20-%20Timing%20Attacks.pdf
Sources
Cache Timing Attacks
At this point, it seems as though we’ve seen everything—there couldn’t possibly be another side-channel attack, right?
Wrong.
Timing attacks are capable of leveraging the CPU cache as a side-channel in order to perform attacks. Since the issue results from hardware design, it’s difficult for application designers to address; the behaviors that influence cache patterns are proprietary features hidden away into today’s processors.
Intel CPU Cache
In cache terminology, hits occur when queried data is present in the cache and misses occur when data must be fetched from main memory. Consider the L1 and L2 caches of the Intel Sandy Bridge processor. Both are 8-way set associative caches consisting of sets with 64-byte lines (64 sets in L1, 512 sets in L2, for a total of 32KB and 256KB in storage, respectively).
For those unfamiliar with computer architecture, addresses of information in the cache are split into three components: tag, set, and offset. An address looks something like this:
1111 0000 1111 0000 1111 000011 110000
Tag Set Offset
Now that we’ve reviewed the memory hierarchy, let’s take a look at some attacks that use variations in cache timing and operation to their advantage.
PRIME+PROBE
The PRIME+PROBE attack is carried out by filling the victim’s cache with controlled data. As the victim carries out normal tasks in their machine, some of the attack data is evicted from the cache. All the while, the attacker monitors the cache contents, keeping careful track of which cache lines were evicted. In doing so, this provides the attacker with intimate knowledge of the operation and nature of the victim’s activities as well as the contents replaced by the victim.
EVICT+TIME
The EVICT+TIME attack is carried out by evicting a line of an AES lookup table from the cache such that all AES lookup tables are in the cache save for one. The attacker then runs the encryption process. As you might imagine, if the encryption process accesses the partially evicted lookup table, encryption will take longer to complete. By timing exactly how long encryption takes, the attackers are able to determine which indices of which tables were accessed. Because table lookups depend on the AES encryption key, the attacker thus gains knowledge about the key.
Cache Games
The Cache Games attack targets AES-128 in OpenSSL v0.9.8 and is capable of recovering the full secret key. In the attack, a non-privileged spy process conducts a 2.8 second observation of approximately 100 AES encryptions (1.56KB of data) and then performs 3 minutes of computation on a separate machine. The spy process is able to abuse the default Linux scheduler, unfortunately named the Completely Fair Scheduler, to monitor cache offset accesses with extremely accurate precision, thus gaining information about the key.
In order to abuse the CFS, the spy process creates hundreds of threads that immediately block. After a few cycles, the first thread awakens, checks for memory accesses by the target code, and then signals for the next thread to awaken. This continues for all threads. To filter-out noise, Cache Games uses an ANN that takes bitmaps of activations and outputs points with high probability of access.

An ANN takes bitmaps of activations and outputs
points with high probability of access
The nature of the AES encryption process—consisting of 10 rounds of 16 memory accesses—allows the spy process to construct a list of partial-key candidates that is continually refined as more encryptions are repeated. The CFS maintains processes in a red-black tree and associates with each process a total runtime. The scheduler calculates a “max execution time” for each process by dividing the total time it has been waiting by the number of processes in the tree. Whichever process minimizes this value is selected to run next.
Mitigation
- Remove or restrict access to high-resolution timers such as
rdtsc(unlikely; necessary to benchmark various hardware properties) - Allow certain memory to be marked as uncacheable (hardware challenge!)
- Use AES-NI instructions in Intel chips to compute AES (but what about other encryption algorithms?)
- Scatter-gather: secret data should not be allowed to influence memory access at coarser-than-cache-line granularity.
CacheBleed
TODO: add paper link
In keeping with the trend of affixing “-bleed” to various information security leakage vulnerabilities, CacheBleed is a recent (c. 2016) attack on RSA decryptions as implemented in OpenSSL v1.0.2 on Intel Sandy Bridge processors. In the attack, the timing of operations in cache banks is taken advantage of in order to glean information about the RSA decryption multiplier.
Cache banks were a new feature in Sandy Bridge processors, designed to accommodate accessing multiple instructions in the same cache line in the same cycle. As it turns out, cache banks can only serve one operation at a time, so if a cache bank conflict is encountered, one request will be delayed!
In order to carry-out the attack, the attacker and victim start out running on the same hyperthreaded core, thus sharing the L1 cache. The attacker then issues a huge number of requests to a single cache bank. By carefully measuring how many cycles passed in completion of the request, the attacker can discern whether the victim accessed that cache bank at some point. After many queries, the attack is successful at extracting both 2048-bit and 4096-bit secret keys.
Mitigation
The upside to CacheBleed is that it’s highly complicated, requiring shared access to a hyperthreaded core on which RSA decryption is taking place—certainly not a predictable scenario. In any case, there are other pieces of “low-hanging fruit” in computer systems that attackers are more likely to target. Nonetheless, Haswell processors implement cache banks differently such that conflicts are handled more carefully. The only other mitigation technique is to disable hyperthreading entirely.
The Cloudflare Leak
How the Incident Developed
Cloudflare is an Internet infrastructure company that provides security and performance services to millions of websites. On February 17th, 2017, Travis Ormandy, a security researcher from Google’s Project Zero, noticed that some HTTP requests running through Cloudflare were returning corrupted web pages.
https://twitter.com/taviso/status/832744397800214528
The problem that Travis noticed was that under certain circumstances, when the Cloudflare “edge servers” returned a web page, they were going past the end of a buffer and adding to the HTML dumps of memory that contained information such as auth tokens, HTTP POST bodies, HTTP cookies, and other private information [1]. To make matters worse, search engines both indexed and cached this data such that it was for a while searchable.

http://pastebin.com/AKEFci31
Since the discovery of the bug, Cloudflare worked with Google and other search engines to remove affected the cached pages.
The Impact
Data could have been leaking as early as September 22nd, but Cloudflare reported that the period of highest impact was from February 13th through February 18th with around 1 in every 3,300,000 HTTP requests have a potential memory leakage [1]. It is difficult to assess how much data was leaked, especially since the corrupted results and their cached versions were quickly removed from search engines, but Wired reported that data from large companies such as Fitbit, Uber, and OKCupid was found in the corrupted pages of a set of affected web pages.
Cloudflare asserts that the leak did not reveal any private keys, and even though other sensitive information was leaked, it did not appear in the HTML content of particularly high-traffic sites, so the damage was mitigated.
Overall, about 3000 customer’s sites triggered the bug, but, as previously noted, the data leaked could have come from any other Cloudflare customer. Cloudflare is aware of about 150 customers who were affected in that way.
The Bug Itself
As mentioned earlier, the problem resulted from a buffer being overrun and thus additional data from memory being written to the HTML of web pages. But how did this happen, and why did it happen now?
Some of Cloudflare’s services rely on modifying, or “rewriting,” HTML pages as they are routed through the edge servers. In order to do this rewriting, Cloudflare reads and parses the HTML to find elements that require changing. Cloudflare used to use a HTML parser written using a project called Ragel that converts a description of a regular language into a finite state machine. However, about a year ago they decided that the Ragel-based parser was a source of technical debt and wrote a new parser called cf-html to replace it [1].
Cloudflare first rolled this new parser our for their Automatic HTTP Rewrites service and have since been slowly migrating other services away from the Ragel-based parser. In order to use these parsers, Cloudflare adds them as a module to NGINX, a load-balancer [1].
As it turned out, the parser that was written with Ragel actually had a bug in it for several years, but there was no memory leak because of a certain configuration fo the internal NGINX buffers. When cf-html was adopted, the buffers slightly changed, enabling the leakage.
The actual bug was caused by what you might expect: a pointer error in the C code generated by Ragel (but the bug was not the fault of Ragel).

https://blog.cloudflare.com/incident-report-on-memory-leak-caused-by-cloudflare-parser-bug/
As can be guessed from this snippit, the cause of the bug was that the check for the end of the bugger was done using the equality operator, ==, instead of >=, which would have caught the bug. That snippit is the generated code. Let’s look at the code that generated that.
In order to check for a the end of the buffer when parsing a <script> tag, this piece of code was used:

https://blog.cloudflare.com/incident-report-on-memory-leak-caused-by-cloudflare-parser-bug/
What it means is that in order to parse the end of the tag, zero or more unquoted_attr_char are parsed followed by whitespace, /, or > signifying the end of the tag. If there is nothing wrong with the script tag, the parser will move to the code in the @{ }. If there is a problem, the parser will move to the $lerr{ } section.
The bug was caused if a web page ended with a malformed HTML tag such as <script type=. The parser would transition to dd("script consume_attr failed") which is just print debug output, but then instead of failing, it transitions to fgoto script_consume_attr;, which means it tries to parse another attribute.
Notice that the @{ } block has a fhold while the $lerr{ } block does not. It was the lack of the fhold in the second block that caused the leak. In the generated code, fhold is equivalent to p-- and thus if the malformed tag error happens at the end of the buffer, then p will actually be after the end of the document and the check for the end of the buffer will fail, causing p to overrun the buffer.
The Response From Cloudflare
Cloudflare seems to have responded relatively well to this bug. After the bug was brought to their attention they performed an initial mitigation, which meant disabling all of the sevices that used cf_html, in 47 minutes. Luckily, Cloudlfare uses a ‘global kill’ [1] feature to enable the global disabling of any service. Since the Email Obfuscation was the main cause of the leak, it was disabled first, and then Automatic HTTPS rewrites were killed about 3 hours later. About 7 hours after the bug was detected, a fix was deployed globablly. As mentioned previously, Cloudflare also contacted search engines to get the affected pages and their cached versions removed from the web.
What was not as good about Cloudflare’s response were the lessons they said they learned in their incident report. Essentially, their lessons learned amounted to saying the bug was a corner case in an “ancient piece of software” and that they will be looking to “fuzz older software” to look for other potential problems [1]. We hope Cloudflare will take more time to look at this incident more seriously and consider systemic issues that could allow such a problem to occur and persist.
Further Thoughts
Bugs like this expose the difficulty of ensuring software correctness. It is quite unlikely that a corner case like this would have been caught by human eyes, and even a fuzzer would have had to have triggered some exceptional conditions in order to exposed the bug. On the other hand, many tools and processes exist for detecting these types of problems, and there is little excuse for not using them on security-critical software.
Reference
[1] https://blog.cloudflare.com/incident-report-on-memory-leak-caused-by-cloudflare-parser-bug/
The First SHA-1 Collision
On February 23rd, 2017, researchers from Google and CWI Institute in Amsterdam) announced the first SHA-1 collision. As proof of this claim, two PDFs were published that yield the same SHA-1 hash despite containing different content (PDF 1, PDF 2).

https://shattered.it/static/shattered.png
While weaknesses in SHA-1 had been known since the work by Xiaoyun Wang and colleagues in 2004, this is the first known attack to find an actual SHA-1 collision. While SHA-1 was deprecated by NIST in 2011, many systems still extensively use SHA-1 (git, SVN, even some certificate authorities, etc.). The researchers argue that these findings should reinforce the need to more secure hashing algorithms:
We hope that our practical attack against SHA-1 will finally convince the industry that it is urgent to move to safer alternatives such as SHA-256.
Attack Details
SHA-1 takes an arbitrary length message and computes a 160-bit hash. It divides the (padded) input into \(k\) blocks \(M_1, M_2, …, M_k\) of 512 bits. The 160-bit internal state \(CV_j\), called the chaining value, is initialized to some initial value \(CV_0 = IV\). Then, each block \(M_j\) is fed to a compression function \(h\) that updates the chaining value, \(CV_{j+1} = h(CV_j, M_{j+1})\). \(CV_k\) Is the output of the hash.
The attack implements the best known theoretical collision attack outlined by Stevens (2013) (one of the leaders of this effort). This attack is an identical-prefix collision attack, where a given prefix \(P\) is extended with two distinct near collision block pairs such that they collide for any suffix \(S\):
$$ \text{SHA-1}(P||M_1^{(1)}||M_2^{(1)}||S) = \text{SHA-1}(P||M_1^{(2)}||M_2^{(2)}||S) $$
Finding both the first and second near collision block pairs, (\(M_1^{(1)}, M_1^{(2)}\)) and (\(M_2^{(1)}, M_2^{(2)}\)), respectively, was completed using slightly modified algorithms from Stevens’ work. Broadly speaking, differences in the first block pair cause a small difference in the output chaining value, which is “canceled” by the difference in the second block pair. The remaining identical suffixes ensure a collision. Differential paths are leveraged as a precise description of the differences in block pairs and how these differences evolve through the hashing steps. This description is the foundation of a search over the possible block pairs. Note that once the collision block pairs are found for a particular prefix, any number of colliding inputs can be found since S can be anything.
The PDF format is exploited by packaging the differing collision blocks into an embedded JPEG image. In the example collision, the differing blocks are aligned such that the background of the PDFs are different.
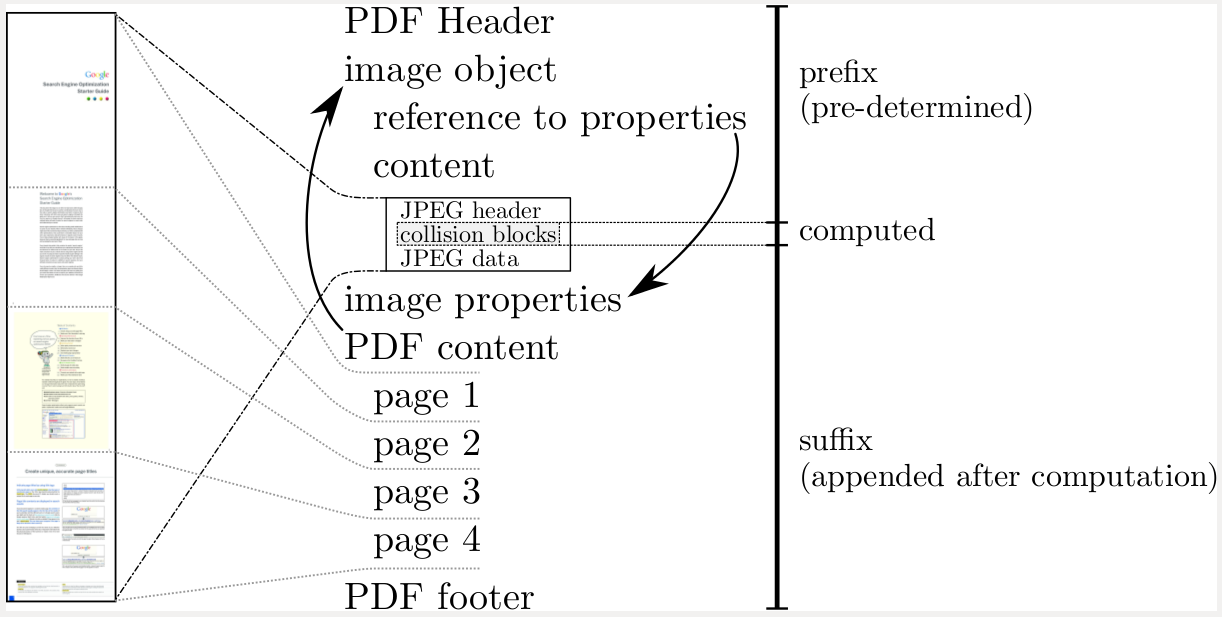
https://shattered.it/static/pdf_format.png
A significant contribution of this work is to apply these algorithms at the scale necessary for practical execution. While the source code for these computations has not yet been released (the authors are allowing a grace period to move to modern hashing algorithms), the changes required to scale this attack are highly non-trivial. Combined, the computations required approximately 6500 CPU years and 100 GPU years. At the time of publishing, the authors estimate the total cost of their attack (via AWS) at $110,000, easily within the reach of criminals. This attack is estimated to be approximately 100,000 times faster than a brute force search.
Full technical details of the attack are outlined in the released paper: Marc Stevens, Elie Bursztein, Pierre Karpman, Ange Albertini, Yarik Markov. The first collision for full SHA-1. (Released 23 February, 2017)