Timing Attacks
Digression: Notable News
Two newsworthy events occurred this week that are of high importance and relevant to TLS in general: SHA-1 Collisions and the Cloudflare Leak. (Those are discussed in the separate linked posts.)
Introduction
Timing attacks exploitd information leaked from timing side-channels to learn private data. In this threat model, an attacker is able to observe the time required for certain parts of a program at runtime and gain information about the execution path followed.
Consider the following snippet of Python code as an example:
def comp(a, b):
if len(a) != len(b):
return False
for c1, c2 in zip (a, b):
if c1 != c2:
return False
return True
The comp() function performs string comparison, returning True if the strings are character-wise equal and False otherwise. Let us assume for the sake of simplicity that the lengths of the strings are public (we are not concerned with timing leaks from the initial length comparison).
Suppose we compare the strings "hello" and "catch". These words fail the string comparison immediately, since the first letters are different. Thus, the function returns False after a single iteration of the loop. In contrast, comparing "hello" with "hella" will require 5 iterations before returning False. An attacker can use the resulting timing delay to determine that "hello" and "hella" share beginning characters, whereas "hello" and "catch" do not. If "hello" was a password, an attacker who could measure the timing precisely enough to count loop iterations would be able to incrementally guess each letter of the string.
One solution to this problem would be to use a Boolean flag initialized to True. If the words have mismatched characters, the flag will be set to False, and the flag will be returned after comparing all characters. In theory, this masks the timing leak; in practice, a compiler may optimize such code to return early, reinstating the timing leak. Furthermore, there may still be timing leaks in the execution of the code, such as variation in the instruction cache depending on which statements are entered.
Thus, we see from this simple example that verifying constant-time implementation of code has many challenges, which we further discuss below.
Remote Timing Attacks are Practical
Remote timing attacks are practical. David Brumley and Dan Boneh (2005).Computer Networks, 48(5), 701-716.]
At the heart of RSA decription is a modular exponentiation \( m = c^d mod~N\) where \(N = pq\) is the RSA modulus, d is the private decryption exponent, and c is the ciphertext being decrypted. OpenSSL uses the Chinese Remainder Theorem (CRT) to perform this exponentiation. With Chinese remaindering, the function \( m = c^d mod~N\) is computed in two steps:
Evaluate \( m_1 = c^{d_1} mod~p\) and \( m_2 = c^{d_2} mod~q\) (\(d_1\) and \(d_2\) are precomputed from \(d\)).
Combine \(m_1\) and \(m_2\) using CRT to yield m.
Both steps could have timing side channels if not implemented carefully.
Chinese Remainder Theorem
Suppose that \(n_1,n_2,…,n_r\) are pairwise relatively prime positive integers, and let \(c_1,c_2,…,c_r\) be integers.
Then the system of congruences,
\(X \equiv c_2 (mod~n_2)\)
…
\(X \equiv c_r (mod~n_r)\)
has a unique solution modulo \(N = n_1n_2…n_r\)
Gauss’s Algorithm
\(X \equiv c_1N_1{N_1}^{-1} + c_2N_2{N_2}^{-1} + … + c_rN_r{N_r}^{-1}(mod~N)\), where
\(N_i{N_1}^{-1} \equiv 1 (mod~n_i)\)
Hasted’s Broadcast Attack
Hasted’s Broadcast Attack relies on cases when the public exponent \(e\) is small or when partial knowledge of the secret key is available. If \(e\) (public) is the same across different sites, the attacker can use Chinese Remainder Theorem and decrypt messages!
Hasted’s Broadcast Attack works as follows:
- Alice encrypts the same message \(M\) with three different public keys \(n_1\) \(n_2\) and \(n_3\)
, all with public exponent \(e=3\), The resulting \(C_1C_2\) and \(C_3\) are known.
\(M^3 \equiv C_1 (mod~n_1)\)
\(M^3 \equiv C_2 (mod~n_2)\)
\(M^3 \equiv C_3 (mod~n_3)\) - An attack can then recover \(M\):
\(x = C_1N_1N_1^{-1} + C_2N_2N_2^{-1} + C_3N_3N_3^{-1}~mod~n_1n_2n_3 \)
\(M = \sqrt[3]{x}\)
Montgomery Reduction
Montgomery Reduction is an algorithm that allows modular arithmetic to be performed efficiently when the modulus is large.
The reduction takes advantage of the fact that \(x~mod~2^n\) is easier to compute than \(x~mod~q\); the reduction simply strips off all but the \(n\) least significant bytes.
Steps needed for the reduction:
The Montgomery Form of \(a\) is \(aR~mod~q\), where \(R\) is some public \(2n , n\) chosen based on underlying hardware.
Multiplication of \(ab\) in Montgomery Form: \(aRbR = cR2\).
Pre-compute \(RR^{-1}~mod~q\).
Reduce: \(cR^{2}R^{-1}~mod~q = cR~mod~q\).
\(c\) can be kept in form and reused for additional multiplications during sliding windows.
To escape Montgomery space and return to \(q\) space: multiply again by \(R^{-1}\) to arrive at solution \(c\).
\(c = ab~mod~q\) (performing \(mod\) by \(q\) causes successive subtractions of \(ab\) by \(q\) till result \(c\) in range \([0,q)\). The number of “extra reductions” depends on the private data; the attack exploits these as a timing side channel.
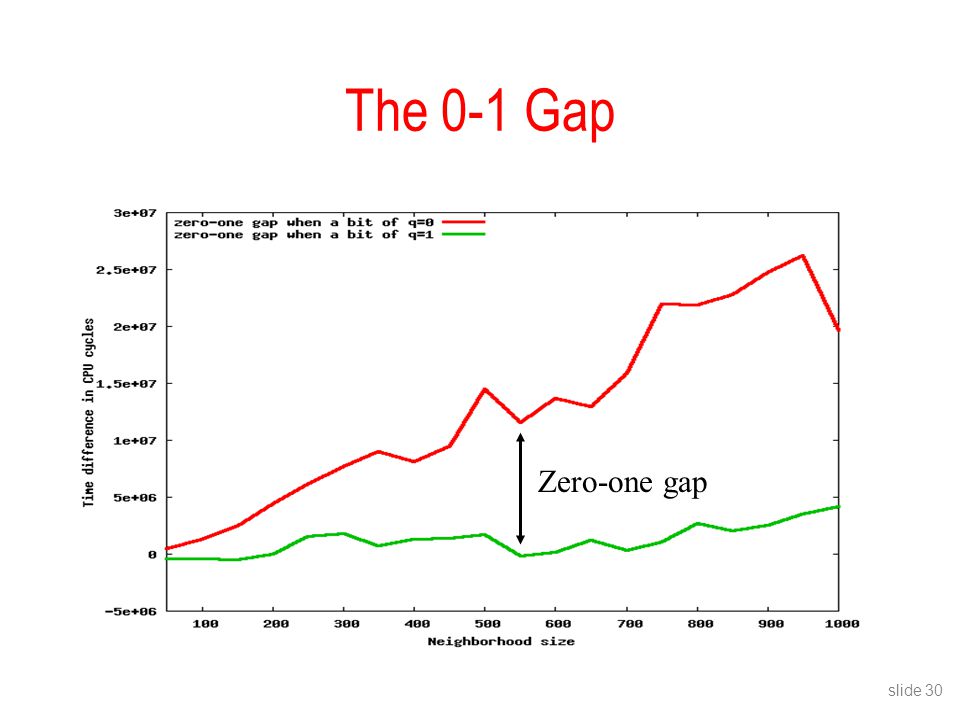
(Image credit)
Protections against timing attacks
There are numerous defenses against timing attacks, but known defenses are either expensive or only provide partial mitigation.
Use a decryption routine with the number of operations is independent of input. For example, simply carry out the maximum number of Montgomery extra reductions, even if they are not necessary. This might be hard to mend to existing systems without replacing their entire decryption algorithm (and it is important to be wary of “overly-optimizing” compilers that remove non-functional code that is there to mask a timing leak).
By quantizing all RSA computations. This decreases performance because “all decryptions must take the maximum time of any decryption”.
By blinding, which works as follows:
- Calculate \(x = reg~mod~N\) before actual decryption for random \(r\) chosen each time
- Decrypt as normal.
- Unblind: divide by \(r~mod~N\) to obtain the decryption of the ciphertext \(g\).
Since \(r\) is random, \(x\) is also random – and input \(g\) should have minimal correlation with total decryption time.
Remote Timing Attacks are Still Practical
Timing attacks target cryptosystems and protocols that do not run in constant time. Elliptic curve based signature schemes aim at providing side-channel resistance against timing attacks. For instance, scalar multiplication is achieved via Montgomery’s ladder which performs a sequence of independent field operations on elliptic curves. Brumley and Tuveri reveal a timing attack vulnerability in OpenSSL’s implementation of Montgomery’s ladder that consequently leaks the server’s private key.
What is Montgomery’s Ladder?
Consider the right-to-left square-and-multiply algorithm to compute an exponentiation operation:
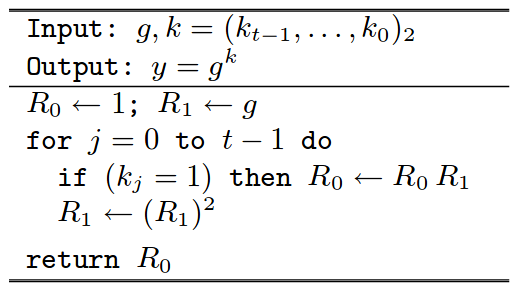
Right-to-Left Square-and-Multiply Algorithm
Source: https://cr.yp.to/bib/2003/joye-ladder.pdf
The above algorithm performs more operations when the bit is set, thereby leading to a possible timing attack. Montgomery’s power ladder method, on the other hand, performs the same number of operations in both the cases. This prevents timing based side-channel attacks as well as makes the algorithm more efficient by making it parallelizable. The algorithm is as below:

Montgomery’s Ladder
Source: https://cr.yp.to/bib/2003/joye-ladder.pdf
OpenSSL’s implementation of Montgomery’s Ladder
OpenSSL uses Elliptic Curve Cryptography for generating Digital Signatures to sign a TLS server’s RSA key. Elliptic Curve Cryptography for Digital Signature uses the following curve for binary fields:
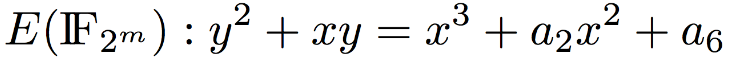
Parties select private key as \(0 < d < n\) and public key as \([d]G\) and then proceed to generate digital signatures using elliptic curves as:
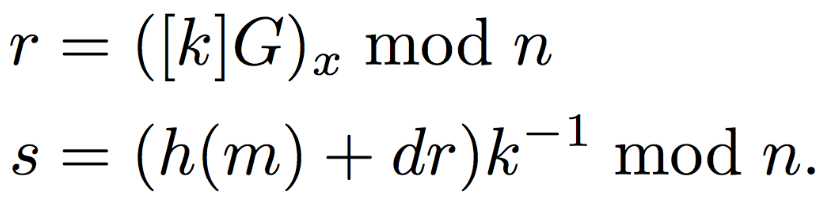
OpenSSL uses Montogmery’s ladder to compute the above digital signatures since it requires multiple exponentiation operations. However, OpenSSL’s implementation has a flaw that leads to timing attack. Below is OpenSSL’s implementation:

OpenSSL’s implementation of Montgomery’s Ladder
Source: https://gnunet.org/sites/default/files/Brumley%20%26%20Tuveri%20-%20Timing%20Attacks.pdf
Countermeasure
A possible countermeasure as proposed by Brumley and Tuveri is to pad the scalar \(k\):
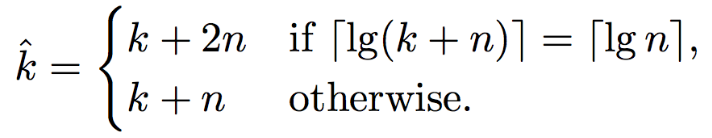
Countermeasure to OpenSSL’s flaw
Source: https://gnunet.org/sites/default/files/Brumley%20%26%20Tuveri%20-%20Timing%20Attacks.pdf
Sources
Cache Timing Attacks
At this point, it seems as though we’ve seen everything—there couldn’t possibly be another side-channel attack, right?
Wrong.
Timing attacks are capable of leveraging the CPU cache as a side-channel in order to perform attacks. Since the issue results from hardware design, it’s difficult for application designers to address; the behaviors that influence cache patterns are proprietary features hidden away into today’s processors.
Intel CPU Cache
In cache terminology, hits occur when queried data is present in the cache and misses occur when data must be fetched from main memory. Consider the L1 and L2 caches of the Intel Sandy Bridge processor. Both are 8-way set associative caches consisting of sets with 64-byte lines (64 sets in L1, 512 sets in L2, for a total of 32KB and 256KB in storage, respectively).
For those unfamiliar with computer architecture, addresses of information in the cache are split into three components: tag, set, and offset. An address looks something like this:
1111 0000 1111 0000 1111 000011 110000
Tag Set Offset
Now that we’ve reviewed the memory hierarchy, let’s take a look at some attacks that use variations in cache timing and operation to their advantage.
PRIME+PROBE
The PRIME+PROBE attack is carried out by filling the victim’s cache with controlled data. As the victim carries out normal tasks in their machine, some of the attack data is evicted from the cache. All the while, the attacker monitors the cache contents, keeping careful track of which cache lines were evicted. In doing so, this provides the attacker with intimate knowledge of the operation and nature of the victim’s activities as well as the contents replaced by the victim.
EVICT+TIME
The EVICT+TIME attack is carried out by evicting a line of an AES lookup table from the cache such that all AES lookup tables are in the cache save for one. The attacker then runs the encryption process. As you might imagine, if the encryption process accesses the partially evicted lookup table, encryption will take longer to complete. By timing exactly how long encryption takes, the attackers are able to determine which indices of which tables were accessed. Because table lookups depend on the AES encryption key, the attacker thus gains knowledge about the key.
Cache Games
The Cache Games attack targets AES-128 in OpenSSL v0.9.8 and is capable of recovering the full secret key. In the attack, a non-privileged spy process conducts a 2.8 second observation of approximately 100 AES encryptions (1.56KB of data) and then performs 3 minutes of computation on a separate machine. The spy process is able to abuse the default Linux scheduler, unfortunately named the Completely Fair Scheduler, to monitor cache offset accesses with extremely accurate precision, thus gaining information about the key.
In order to abuse the CFS, the spy process creates hundreds of threads that immediately block. After a few cycles, the first thread awakens, checks for memory accesses by the target code, and then signals for the next thread to awaken. This continues for all threads. To filter-out noise, Cache Games uses an ANN that takes bitmaps of activations and outputs points with high probability of access.

An ANN takes bitmaps of activations and outputs
points with high probability of access
The nature of the AES encryption process—consisting of 10 rounds of 16 memory accesses—allows the spy process to construct a list of partial-key candidates that is continually refined as more encryptions are repeated. The CFS maintains processes in a red-black tree and associates with each process a total runtime. The scheduler calculates a “max execution time” for each process by dividing the total time it has been waiting by the number of processes in the tree. Whichever process minimizes this value is selected to run next.
Mitigation
- Remove or restrict access to high-resolution timers such as
rdtsc(unlikely; necessary to benchmark various hardware properties) - Allow certain memory to be marked as uncacheable (hardware challenge!)
- Use AES-NI instructions in Intel chips to compute AES (but what about other encryption algorithms?)
- Scatter-gather: secret data should not be allowed to influence memory access at coarser-than-cache-line granularity.
CacheBleed
TODO: add paper link
In keeping with the trend of affixing “-bleed” to various information security leakage vulnerabilities, CacheBleed is a recent (c. 2016) attack on RSA decryptions as implemented in OpenSSL v1.0.2 on Intel Sandy Bridge processors. In the attack, the timing of operations in cache banks is taken advantage of in order to glean information about the RSA decryption multiplier.
Cache banks were a new feature in Sandy Bridge processors, designed to accommodate accessing multiple instructions in the same cache line in the same cycle. As it turns out, cache banks can only serve one operation at a time, so if a cache bank conflict is encountered, one request will be delayed!
In order to carry-out the attack, the attacker and victim start out running on the same hyperthreaded core, thus sharing the L1 cache. The attacker then issues a huge number of requests to a single cache bank. By carefully measuring how many cycles passed in completion of the request, the attacker can discern whether the victim accessed that cache bank at some point. After many queries, the attack is successful at extracting both 2048-bit and 4096-bit secret keys.
Mitigation
The upside to CacheBleed is that it’s highly complicated, requiring shared access to a hyperthreaded core on which RSA decryption is taking place—certainly not a predictable scenario. In any case, there are other pieces of “low-hanging fruit” in computer systems that attackers are more likely to target. Nonetheless, Haswell processors implement cache banks differently such that conflicts are handled more carefully. The only other mitigation technique is to disable hyperthreading entirely.